The Quadratic Law of Reciprocity and the Theory of Galois Fields

Extract

The theory of quadratic congruences modulo an integer is dominated by the Quadratic Law of Reciprocity (see § 1), which makes it possible to decide in a very short time whether a quadratic congruence

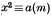
is solvable or not. The law was first proved by Gauss.* It took him over a year to obtain his first proof, which depends on a tedious lemma in elementary number theory. He subsequently obtained seven further proofs, and today more than fifty proofs are known, most of them based on the ideas of Gauss. The object of the present paper is to present a proof which is a modernised version of Gauss's seventh proof, applying the ideas of that proof to a finite set of objects, the elements of a finite or Galois field.