Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T17:45:08.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Property (T) in k-gonal random groups

Part of: Probabilistic methods in group theory Special aspects of infinite or finite groups

Published online by Cambridge University Press:  22 February 2022

MurphyKate Montee
MurphyKate Montee*
Affiliation:
Department of Mathematics and Statistics, Carleton College, Northfield, MN 55057, USA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The k-gonal models of random groups are defined as the quotients of free groups on n generators by cyclically reduced words of length k. As k tends to infinity, this model approaches the Gromov density model. In this paper, we show that for any fixed 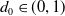$d_0 \in (0, 1)$ , if positive k-gonal random groups satisfy Property (T) with overwhelming probability for densities 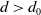$d >d_0$ , then so do jk-gonal random groups, for any 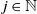$j \in \mathbb{N}$ . In particular, this shows that for densities above 1/3, groups in 3k-gonal models satisfy Property (T) with probability 1 as n approaches infinity.

Keywords

random groupsproperty (T)

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20P05: Probabilistic methods in group theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 3 , September 2022 , pp. 734 - 738
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashcroft, C. J. and Roney-Dougal, C. M., On random presentations with fixed relator length, Comm. Algebra 48(5) (2020), 1904–1918. ISSN: 0092-7872. doi: 10.1080/00927872.2019.1710161. Available at https://doi.org/10.1080/00927872.2019.1710161.CrossRefGoogle Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazh-dan’s property (T) , New Mathematical Monographs, vol. 11 (Cambridge University Press, Cambridge, 2008), arxiv+472. ISBN: 978-0-521-88720-5. doi: 10.1017/CBO9780511542749. Available at https://doi.org/10.1017/CBO9780511542749.Google Scholar
Gromov, M., Asymptotic invariants of infinite groups, in Geometric group theory, Vol. 2 (Sussex, 1991), London Mathematical Society Lecture Note Series, vol. 182 (Cambridge University Press, Cambridge, 1993), 1–295.Google Scholar
Kazdan, D. A., On the connection of the dual space of a group with the structure of its closed subgroups, Funkcional. Anal. i Prilozen. 1 (1967), 71–74. ISSN: 0374-1990.Google Scholar
Kotowski, M. and Kotowski, M., Random groups and property (T): Żuk’s theorem revisited, J. Lond. Math. Soc. (2) 88(2) (2013), 396–416. ISSN: 0024-6107. doi: 10.1112/jlms/jdt024. Available at https://doi.org/10.1112/jlms/jdt024.CrossRefGoogle Scholar
Lubotzky, A., Discrete groups, expanding graphs and invariant measures, Progress in Mathematics, vol. 125. With an appendix by Jonathan D. Rogawski (Birkhauser Verlag, Basel, 1994), xii+195. ISBN: 3-7643-5075-X. doi: 10.1007/978-3-0346-0332-4. Available at https://doi.org/10.1007/978-3-0346-0332-4.Google Scholar
Mackay, J. M. and Przytycki, P., Balanced walls for random groups, Michigan Math. J. 64(2) (2015), 397–419. ISSN: 0026-2285. doi: 10.1307/mmj/1434731930. Available at https://doi.org/10.1307/mmj/1434731930.CrossRefGoogle Scholar
Montee, M., Cubulating random groups at densities less than 3/14 (in preparation) arXiv: 2106.14931.Google Scholar
Odrzygozdz, T., Bent walls for random groups in the square and hexagonal model (2019). arXiv: 1906.05417 [math.GR].Google Scholar
Ollivier, Y., Sharp phase transition theorems for hyperbolicity of random groups, Geom. Funct. Anal. 14(3) (2004), 595–679. ISSN: 1016-443X. doi: 10.1007/s00039-004-0470-y. Available at https://doi.org/10.1007/s00039-004-0470-y.CrossRefGoogle Scholar
Ollivier, Y., A January 2005 invitation to random groups, EnsaiosMatematicos [Mathematical Surveys], vol. 10 (Sociedade Brasileira de Matematica, Rio de Janeiro, 2005), ii+100. ISBN: 85-85818-30-1.CrossRefGoogle Scholar
Ollivier, Y., Some small cancellation properties of random groups, Int. J. Algebra Comput. 17(1) (2007), 37–51. ISSN: 0218-1967. doi: 10.1142/S021819670700338X. Available at https://doi.org/10.1142/S021819670700338X.CrossRefGoogle Scholar
Ollivier, Y. and Wise, D. T., Cubulating random groups at density less than 1=6, Trans. Amer. Math. Soc. 363(9) (2011), 4701–4733. ISSN: 0002-9947. doi: 10.1090/S0002-947-12011-05197-4. Available at https://doi.org/10.1090/S0002-9947-2011-05197-4.Google Scholar
Żuk, A., Property (T) and Kazhdan constants for discrete groups, Geom. Funct. Anal. 13(3) (2003), 643–670. ISSN: 1016-443X. doi: 10.1007/s00039-003-0425-8. Available at https://doi.org/10.1007/s00039-003-0425-8.Google Scholar