Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T10:05:07.815Z Has data issue: false hasContentIssue false
  • English
  • Français

PROPERTIES OF CERTAIN SUBALGEBRAS OF DALES-DAVIE ALGEBRAS

Published online by Cambridge University Press:  09 August 2007

M. ABTAHI  and
T. G. HONARY
M. ABTAHI
Affiliation:
Faculty of Mathematical Sciences and Computer Engineering, Teacher Training University, Tehran, 15618, I.R. Iran e-mails: [email protected], [email protected]
T. G. HONARY
Affiliation:
Faculty of Mathematical Sciences and Computer Engineering, Teacher Training University, Tehran, 15618, I.R. Iran e-mails: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study an interesting class of Banach function algebras of infinitely differentiable functions on perfect, compact plane sets. These algebras were introduced by H. G. Dales and A. M. Davie in 1973, called Dales-Davie algebras and denoted by D(X, M), where X is a perfect, compact plane set and M = {M n }∞ n = 0 is a sequence of positive numbers such that M 0 = 1 and (m + n)!/M m+n ≤ (m!/M m )(n!/M n ) for m, n ∈ N. Let d = lim sup(n!/Mn )1/n and Xd = {z ∈ C : dist(z, X) ≤ d}. We show that, under certain conditions on X, every f ∈ D(X, M) has an analytic extension to X d . Let DP [D R ]) be the subalgebra of all f ∈ D(X, M) that can be approximated by the restriction to X of polynomials [rational functions with poles off X]. We show that the maximal ideal space of D P is 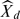, the polynomial convex hull of X d , and the maximal ideal space of D R is X d . Using some formulae from combinatorial analysis, we find the maximal ideal space of certain subalgebras of Dales-Davie algebras.

Keywords

Primary 46J1046J15Secondary 46J20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 49 , Issue 2 , May 2007 , pp. 225 - 233
Copyright
Copyright © Glasgow Mathematical Journal Trust 2007

References

REFERENCES

1. Abramowitz, M. and Stegun, I., Handbook of mathematical functions with formulas, graphs and mathematical tables (U.S. Department of Commerce, Washington, D.C., 1964).Google Scholar
2. Bland, W. J. and Feinestein, J. F., Completion of normed algebras of differentiable functions, Studia Mathematica 170 (2005), 89–111.CrossRefGoogle Scholar
3. Dales, H. G., Banach algebras and automatic continuity, London Mathematical Society Monographs, New Series No. 24 (Oxford University Press).Google Scholar
4. Dales, H. G. and Davie, A. M., Quasi-analytic Banach function algebras, J. Functional Analysis 13 (1973), 28–50.CrossRefGoogle Scholar
5. Honary, T. G., Relations between Banach function algebras and their uniform closusres, Proc. Amer. Math. Soc. 109 (1990), 337–342.CrossRefGoogle Scholar