Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T04:01:07.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Prime ideals of quantized Weyl algebras

Published online by Cambridge University Press:  18 May 2009

M. Akhavizadegan  and
D. A. Jordan
M. Akhavizadegan
Affiliation:
School of Mathematics and Statistics, Pure Mathematics Section, University of Sheffield, The Hicks Building, Sheffield S3 7RH, UK
D. A. Jordan
Affiliation:
School of Mathematics and Statistics, Pure Mathematics Section, University of Sheffield, The Hicks Building, Sheffield S3 7RH, UK
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main object of study in this paper is the quantized Weyl algebra 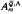which arises from the work of Maltsiniotis [10] on noncommutative differential calculus. This algebra has been studied from the point of view of noncommutative ring theory by various authors including Alev and Dumas [1], the second author [9], Cauchon [3], and Goodearl and Lenagan [5]. In [9], it is shown that 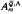has n normal elements zi and, subject to a condition on the parameters, the localization 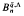obtained on inverting these elements is simple of Krull and global dimension n. It is easy to show that each of these normal elements generates a height one prime ideal and that these are all the height one prime ideals of 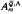. The purpose of this paper is to determine, under a stronger condition on the parameters, all the prime ideals of 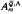and to compare the prime spectrum with that of a related algebra 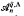. This algebra has more symmetric defining relations than those of 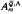but it shares the same simple localization 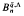which again is obtained by inverting n normal elements zi. Like 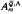the alternative algebra can be regarded as an algebra of skew differential (or difference) operators on the coordinate ring of quantum n-space.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 3 , September 1996 , pp. 283 - 297
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Alev, J. and Dumas, F., Sur le corps des fractions de certaines algèbres quantiques, J. Algebra 170 (1994), 229–265.CrossRefGoogle Scholar
2.Bryant, V. W., Aspects of combinatorics (Cambridge University Press, 1993).Google Scholar
3.Cauchon, G., Quotient premiers de Oq (Mn (k)), preprint, Université de Reims.Google Scholar
4.Goodearl, K. R., Prime ideals in skew polynomial rings and quantized Weyl algebras, J. Algebra 150 (1992), 324–377.CrossRefGoogle Scholar
5.Goodearl, K. R. and Lenagan, T. H., Catenarity in quantum algebras, preprint, Universities of California (Santa Barbara) and Edinburgh.CrossRefGoogle Scholar
6.Goodearl, K. R. and Letzter, E. S., Prime ideals in skew and q-skew polynomial rings, Mem. Amer. Math. Soc. 109 (1994), no. 521.Google Scholar
7.Goodearl, K. R. and Warfield, R. B. Jr, An introduction to noncommutative Noetherian rings (Cambridge University Press, 1989).Google Scholar
8.Jordan, D. A., Normal elements and completions of non-commutative Noetherian rings, Bull. London Math. Soc. 19 (1987), 417–424.CrossRefGoogle Scholar
9.Jordan, D. A., A simple localization of the quantized Weyl algebra, J. Algebra 174 (1995), 267–281.CrossRefGoogle Scholar
10.Maltsiniotis, G., Groupes quantique et structures diffdrentielles, C.R. Acad. Sci. Paris Sir. I Math. 311 (1990), 831–834.Google Scholar
11.McConnell, J. C. and Pettit, J. J., Crossed products and multiplicative analogues of Weyl algebras, J. London Math. Soc. (2) 38 (1988), 47–55.CrossRefGoogle Scholar
12.McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings (Wiley, 1987).Google Scholar
13.Oh, S.Q., Primitive ideals of the coordinate ring of quantum symplectic space, J. Algebra 174 (1995), 531–552.CrossRefGoogle Scholar
14.Rigal, L., Spectre de l'algèbre de Weyl quantique, preprint, Université de Paris VI (1994).Google Scholar