Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T20:59:05.865Z Has data issue: false hasContentIssue false
  • English
  • Français

PINCHING THEOREMS FOR TOTALLY REAL MINIMAL SUBMANIFOLDS IN CPn

Published online by Cambridge University Press:  01 May 2009

CENGİZHAN MURATHAN  and
CİHAN ÖZGÜR
CENGİZHAN MURATHAN
Affiliation:
Department of Mathematics, Uludağ University, 16059, Bursa, Turkey e-mail: [email protected]
CİHAN ÖZGÜR
Affiliation:
Department of Mathematics, Balıkesir University, 10145, Balıkesir, Turkey e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be an n-dimensional totally real minimal submanifold in CPn. We prove that if M is semi-parallel and the scalar curvature τ, 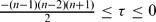, then M is an open part of the Clifford torus Tn ⊂ CPn. If M is semi-parallel and the scalar curvature τ, 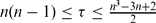, then M is an open part of the real projective space RPn.

Keywords

53C4253C4053C20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 2 , May 2009 , pp. 331 - 339
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Amarzaya, A. and Ohnita, Y., Hamiltonian stability of certain minimal Lagrangian submanifolds in complex projective spaces, Tohoku Math. J. 55 (4) (2003), 583–610.CrossRefGoogle Scholar
2.Calabi, E., Improper affine hyperspheres of convex type and a generalization of a theorem by K. Jörgens, Mich. Math. J. 5 (1958), 105–126.CrossRefGoogle Scholar
3.Chen, B. Y. and Ogiue, K., On totally real submanifolds, Trans. Am. Math. Soc. 193 (1974), 257–266.CrossRefGoogle Scholar
4.Deprez, J., Semi-parallel surfaces in Euclidean space, J. Geom. 25 (1985), 192–200.CrossRefGoogle Scholar
5.Deprez, J., Semi-parallel hypersurfaces, Rend. Sem. Mat. Univers. Politecn. Torino, 44 (1986), 303–316.Google Scholar
6.Dillen, F., Semi-parallel hypersurfaces of a real space form, Israel J. Math. 75 (1991), 193–202.CrossRefGoogle Scholar
7.Ejiri, N., Totally real minimal submanifolds in a complex projective space, Proc. Am. Math. Soc. 86 (1982), no. 3, 496–497.CrossRefGoogle Scholar
8.Ferus, D., Immersions with parallel second fundamental form, Math. Z. 140 (1974), 87–93.CrossRefGoogle Scholar
9.Li, A. M. and Zhao, G., Totally real minimal submanifolds in CP n, Arch. Math. (Basel) 62 (1994), 562–568.CrossRefGoogle Scholar
10.Lumiste, Ü., Semi-symmetric submanifolds as the second order envelope of symmetric submanifolds, Proc. Eston. Acad. Sci. Phys. Math. 39 (1990), 1–8.Google Scholar
11.Naitoh, H., Totally real parallel submanifolds in P n(C), Tokyo J. Math. 4 (2) (1981), 279–306.CrossRefGoogle Scholar
12.Perrone, D., n-dimensional totally real minimal submanifolds of CP n, Arch. Math. (Basel) 68 (1997), 347–352.CrossRefGoogle Scholar
13.Takeuchi, M., Parallel submanifolds of space forms, Manifolds and Lie groups (Notre Dame, IN, 1980), pp. 429–447, Progr. Math., 14 (Birkh äuser, Boston, MA, 1981).CrossRefGoogle Scholar
14.Yano, K. and Kon, M., Anti-invariant submanifolds, Lecture Notes in Pure and Applied Mathematics, No. 21. (Marcel Dekker, New York and Basel, 1976).Google Scholar
15.Yano, K. and Kon, M., Structures on manifolds, Series in Pure Mathematics, 3. (World Scientific, Singapore, 1984).Google Scholar