Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T02:30:57.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Orientable and non-orientable Klein surfaces with maximal symmetry

Published online by Cambridge University Press:  18 May 2009

David Singerman
David Singerman
Affiliation:
University of Southampton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a bordered Klein surface, by which we mean a Klein surface with non-empty boundary. X is characterized topologically by its orientability, the number k of its boundary components and the genus p of the closed surface obtained by filling in all the holes. The algebraic genus g of X is defined by

.

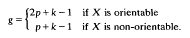If g≥2 it is known that if G is a group of automorphisms of X then |G|≤12(g-l) and that the upper bound is attained for infinitely many values of g ([4], [5]). A bordered Klein surface for which this upper bound is attained is said to have maximal symmetry. A group of 12(g-l) automorphisms of a bordered Klein surface of algebraic genus g is called an M*-group and it is known that a finite group G is an M*-group if and only if it is generated by 3 non-trivial elements T1, T2, T3 which obey the relations

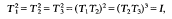
([4]).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 26 , Issue 1 , January 1985 , pp. 31 - 34
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Chetiya, B. P., Groups of automorphisms of compact Riemann surfaces. Ph.D. thesis. University of Birmingham, 1971.Google Scholar
2.Greenleaf, N. and May, C. L., Bordered Klein surfaces with maximal symmetry. Trans. Amer. Math. Soc. 274 (1982) 265–283.CrossRefGoogle Scholar
3.Macbeath, A. M., Generators of the linear fractional groups. Proc. Symp. Pure Math. (Houston, 1967).Google Scholar
4.May, C. L., Automorphisms of compact Klein surfaces with boundary. Pacific J. Math. 59 (1975) 199–210.Google Scholar
5.May, C. L., Large automorphism groups of compact Klein surfaces with boundary. Glasgow Math. J. 18 (1977) 1–10.Google Scholar
6.Singerman, D., Automorphisms of compact non-orientable Riemann surfaces. Glasgow Math. J. 12 (1971) 50–59.Google Scholar