Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T20:23:30.427Z Has data issue: false hasContentIssue false
  • English
  • Français

On the values of the Epstein zeta function

Published online by Cambridge University Press:  18 May 2009

John Roderick Smart
John Roderick Smart
Affiliation:
University of Wisconsin, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ζ(s) = σn-s (Res >1) denote the Riemann zeta function; then, as is well known, 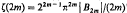, where Bm denotes the mth Bernoulli number, In this paper we investigate the possibility of similar evaluations of the Epstein zeta function ζq(s) at the rational integers s = k> 2. Let

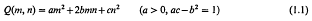
be a positive definite quadratic form and

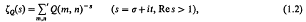
where the summation is over all pairs of integers except (0, 0). In attempting to evaluate ζq(k) we are guided by Kronecker's first limit formula [11]

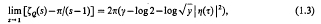
where γ is Euler's constant,

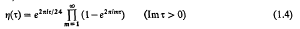
is the Dedekind eta-function, and τ is the complex number in the upper half plane, ℋ, associated with Q by the formula

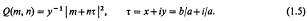
On the basis of (1.3) we would expect a formula involving functions of τ. This formula is stated in Theorem 1, (2.13).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 14 , Issue 1 , February 1973 , pp. 1 - 12
Copyright
Copyright © Glasgow Mathematical Journal Trust 1973

References

REFERENCES

1.Abromowitz, M. and Stegun, I. A., editors, Handbook of mathematical functions, National Bureau of Standards, Applied Mathematics Series 55 (Washington, 1964).Google Scholar
2.Bateman, P. T. and Grosswald, E., On Epstein's zeta function, Acta Arith. 9 (1964), 365–373.CrossRefGoogle Scholar
3.Chowla, S. and Selberg, A., On Epstein's zeta function, J. Reine Angew. Math. 227 (1967), 86–110.Google Scholar
4.Grosswald, E., Die Werte der Riemannschen Zetafunktion an ungeraden Argumentstellen, Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. IIa (1970, Nr. 2), 9–13.Google Scholar
5.Gunning, R. C., Lectures on modular forms, Ann. of Math. Studies 48 (Princeton, 1962).CrossRefGoogle Scholar
6.Hecke, E., Algebraische Zahlen (New York, 1948).Google Scholar
7.Lehner, J., Discontinuous groups and automorphic functions, Amer. Math. Soc. Math. Surveys No. 8 (Providence, R.I., 1964).CrossRefGoogle Scholar
8.Ramanujan, S., Collected papers (Cambridge, 1927).Google Scholar
9.Rankin, R. A., A minimum problem for the Epstein zeta function, Proc. Glasgow Math. Assoc. (1953), 149–158.CrossRefGoogle Scholar
10.Sansone, G. and Gerretson, J., Lectures on the theory of functions of a complex variable I (Groningen, 1960).Google Scholar
11.Siegel, C. L., Lectures on advanced analytic number theory (Tata Institute, Bombay, 1961).Google Scholar
12.Watson, G. N., Theorems stated by Ramanujan II, J. London Math. Soc. 3 (1928), 216–225.CrossRefGoogle Scholar
13.Watson, G. N., Theory of Bessel functions (Cambridge, 1966).Google Scholar