Article contents
On the spectrum of an integral operator
Published online by Cambridge University Press: 18 May 2009
Extract
The integral operator which we will consider in this paper is the operator T denned for suitably restricted functions f on (0, ∞) by
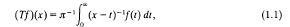
where x >0 and the integral is taken in the Cauchy principal value sense at t = x. This operator plays a considerable role in Wiener–Hopf theory; see [2; Chapter 5].
Since T is clearly the restriction to (0, ∞) of minus the Hilbert transformation applied to functions which vanish on (−∞, 0), it follows easily from the theory of the Hilbert transformation, as given in say [6; Theorem 101], that T is a bounded operator from Lp(0, ∞) to itself for 1 < p < ∞.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1986
References
REFERENCES
- 3
- Cited by


