Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T08:08:10.942Z Has data issue: false hasContentIssue false
  • English
  • Français

On the non-albelian tensor square of a nilpotent group of class two

Published online by Cambridge University Press:  18 May 2009

Michael R. Bacon
Michael R. Bacon
Affiliation:
Department of Mathematics, Binghamton University, Binghamton, Ny 13902-6000, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The nonabelian tensor square G⊗G of a group G is generated by the symbols g⊗h, g, h ∈ G, subject to the relations

,

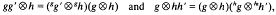
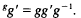for all g, g′, h, h′ ∈ G, where The tensor square is a special case of the nonabelian tensor product which has its origins in homotopy theory. It was introduced by R. Brown and J. L. Loday in [4] and [5], extending ideas of Whitehead in [6].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 3 , September 1994 , pp. 291 - 296
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Aboughazi, R., Produit tensoriel du group d'Heisenberg, Bull. Soc. Math. France 115 (1987), 95–106.Google Scholar
2.Bacon, M. and Kappe, L.-C., The nonabelian tensor square of a 2-generator p-group of class 2, Arch. Math. (Basel) 61 (1993), 508–516.Google Scholar
3.Brown, R., Johnson, D. L., and Robertson, E. F., Some computations of nonabelian tensor products of groups, J. Algebra 111 (1987), 177–202.Google Scholar
4.Brown, R. and Loday, J.-L., Excision homotopique en basse dimension, C. R. Acad. Sci. Paris Sér. I Math. 298 (1984), 353–356.Google Scholar
5.Brown, R. and Loday, J.-L., Van Kampen theorems for diagrams of spaces, Topology 26 (1987), 311–335.CrossRefGoogle Scholar
6.Whitehead, J. H. C., A certain exact sequence, Ann. of Math. 52 (1950), 51–110.Google Scholar