Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T21:31:26.554Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DIOPHANTINE EQUATION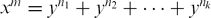

Published online by Cambridge University Press:  01 January 2009

TOMOHIRO YAMADA
TOMOHIRO YAMADA*
Affiliation:
Department of Mathematics, Faculty of Science, Kyoto University, Kyoto, 606-8502, Japan E-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We find all solutions of 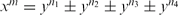in integers m, n1, n2, n3, n4 for all relatively prime integers x, y below 100.

Keywords

11A0511A25
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 1 , January 2009 , pp. 143 - 148
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Baker, A. and Davenport, H., The equations 3x 2 − 2 = y 2 and 8x 2 − y = z 2, Quart. J. Math. 20 (1969), 129–137.CrossRefGoogle Scholar
2.Dede, M. and Tijdeman, R., Exponential diophantine equations with four terms, Indag. Math. N.S. 3 (1992), 47–57.Google Scholar
3.Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, 5th ed. (The Claredon Press, Oxford University Press, New York, 1979).Google Scholar
4.Nagell, T., Introduction to number theory, 2nd ed. (Chelsea Publishing Co., New York, 1964).Google Scholar
5.Senge, H. G. and Strauss, E. G., P. V. numbers and sets of multiplicity, Period Math. Hungar. 3 (1973), 93–100.CrossRefGoogle Scholar
6.Stewart, C. L., On the representation of an integer in two different bases, J. Reine. Angew. Math. 319 (1980), 63–72.Google Scholar
7.Tijdeman, R. and Wang, Lianxiang, Sums of products of powers of given prime numbers, Pacific J. Math. 132 (1988), 177–193, Corr. 135 (1988), 396–398.CrossRefGoogle Scholar
8.Lianxiang, Wang, Four terms equations, Indag. Math. 51 = Proc. K. N. A. W. Ser. A 92 (1989), 355–361.Google Scholar
9.de Weger, B. M. M., Solving exponential diophantine equations using lattice basis reduction algorithms, J. Number Theory 26 (1987), 325–367.CrossRefGoogle Scholar