Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-08T15:27:43.506Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE COMPLEXITY OF FINDING A NECESSARY AND SUFFICIENT CONDITION FOR BLASCHKE-OSCILLATORY EQUATIONS

Part of: Function theory on the disc Differential equations in the complex domain

Published online by Cambridge University Press:  17 December 2014

JANNE HEITTOKANGAS  and
ATTE REIJONEN
JANNE HEITTOKANGAS
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, P.O. Box 111, 80101 Joensuu, Finland e-mails: [email protected], [email protected]
ATTE REIJONEN
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, P.O. Box 111, 80101 Joensuu, Finland e-mails: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If A(z) belongs to the Bergman space 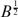, then the differential equation f″+A(z)f=0 is Blaschke-oscillatory, meaning that the zero sequence of every nontrivial solution satisfies the Blaschke condition. Conversely, if A(z) is analytic in the unit disc such that the differential equation is Blaschke-oscillatory, then A(z) almost belongs to 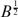. It is demonstrated that certain “nice” Blaschke sequences can be zero sequences of solutions in both cases when A ∈ 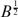or A ∉ 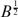. In addition, no condition regarding only the number of zeros of solutions is sufficient to guarantee that A ∈ .

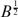MSC classification

Primary: 34M10: Oscillation, growth of solutions
Secondary: 30J10: Blaschke products
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 57 , Issue 3 , September 2015 , pp. 543 - 554
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Buckley, S., Koskela, P. and Vukotić, D., Fractional integration, differentiation, and weighted Bergman spaces, Math. Proc. Camb. Phil. Soc. 126 (2) (1999), 369–385.CrossRefGoogle Scholar
2.Carleson, L., An interpolation problem for bounded analytic functions Am. J. Math. 80 (1958), 921–930.CrossRefGoogle Scholar
3.Chuaqui, M., Gröhn, J., Heittokangas, J. and Rättyä, J., Zero separation results for solutions of second order linear differential equations, Adv. Math. 245 (2013), 382–422.CrossRefGoogle Scholar
4.Duren, P., Theory of Hp spaces (Academic Press, New York, 1970).Google Scholar
5.Duren, P. and Schuster, A., Bergman Spaces, Mathematical Surveys and Monographs, vol. 100 (American Mathematical Soc., Providence, 2004).Google Scholar
6.Fricain, E. and Mashreghi, J., Integral means of the derivatives of Blaschke products, Glasg. Math. J. 50 (2) (2008), 233–249.CrossRefGoogle Scholar
7.Gotoh, Y., On integral means of the derivatives of Blaschke products, Kodai Math. J. 30 (1) (2007), 147–155.CrossRefGoogle Scholar
8.Gröhn, J. and Heittokangas, J., New findings on Bank-Sauer approach in oscillation theory Constr. Approx. 35 (2012), 345–361.CrossRefGoogle Scholar
9.Hedenmalm, H., Korenblum, B. and Zhu, K., Theory of Bergman spaces, Graduate Texts in Mathematics, vol. 199 (Springer, New York, 2000).Google Scholar
10.Heittokangas, J., A survey on Blaschke-oscillatory differential equations, with updates, in Blaschke products and their applications, Fields Inst. Commun. vol. 65 (Fricain, E. and Mashreghi, J., Editors) (Springer, New York, 2013), 43–98.Google Scholar
11.Heittokangas, J., Solutions of f” + A(z)f = 0 in the unit disc having Blaschke sequences as the zeros, Comput. Methods Funct. Theory 5 (1) (2005), 49–63.CrossRefGoogle Scholar
12.Heittokangas, J. and Laine, I., Solutions of f” + A(z)f = 0 with prescribed sequences of zeros, Acta Math. Univ. Comen. 124 (2) (2005), 287–307.Google Scholar
13.Heittokangas, J., Korhonen, R. and Rättyä, J., Linear differential equations with coefficients in weighted Bergman and Hardy spaces, Trans. Am. Math. Soc. 360 (2008), 1035–1055.CrossRefGoogle Scholar
14.Kim, H., Derivatives of Blaschke products, Pac. J. Math. 114 (1) (1984), 175–190.CrossRefGoogle Scholar
15.Linden, C., Hp-derivatives of Blaschke products, Mich. Math. J. 23 (1976), 43–51.CrossRefGoogle Scholar
16.Nehari, Z., The Schwarzian derivative and Schlicht functions Bull. Am. Math. Soc. 55 (1949), 545–551.CrossRefGoogle Scholar
17.Pommerenke, Ch., On the mean growth of the solutions of complex linear differential equations in the disk, Complex Var. Theory Appl. 1 (1) (1982), 23–38.Google Scholar
18.Protas, D., Blaschke products with derivative in Hp and Bp Mich. Math. J. 20 (1973), 393–396.Google Scholar
19.Šeda, V., On some properties of solutions of the differential equation y” + Ay = 0 with solutions having the prescribed zeros, Acta Fac. Nat. Univ. Comen. Math. 4 (1959), 223–253. (Slovak)Google Scholar
20.Yamashita, S., Gap series and α-Bloch functions, Yokohama Math. J. 28 (1980), 31–36.Google Scholar