Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-12T12:19:09.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On the approximation of π by special algebraic numbers

Published online by Cambridge University Press:  18 May 2009

Erhard Braune
Erhard Braune
Affiliation:
A-4020 Linz/D, Lannergasse 16, Austria
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that m0 is an integer, m0≥3, ρ = exp(2πi/m0), K = ℚ(ρ, i), v denotes the degree of K, ξ∈K has degree N over ℚ. The length, 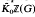where 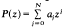is the (irreducible) minimal polynomial for with ξ relatively prime integer coefficients. Feldman [2, p. 49] proved that there is an absolute constant c0>0 such that

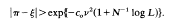
From [2, p. 49, Notes 1 and 2] we know that v = φ(m0) or v = 2φ(m0), and φ(m0)≥ c1m0(log log m0)−1 (c1 > an absolute constant), where φ(m0) denotes Euler's function.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 21 , Issue 1 , January 1980 , pp. 51 - 56
Copyright
Copyright © Glasgow Mathematical Journal Trust 1980

References

REFERENCES

1.Cijsouw, P. L., A transcendence measure for π, Transcendence theory: advances and applications, Proc. of a conference in Cambridge 1976 (Ed. Baker, A. and Masser, D. W.), (Academic Press, 1977).Google Scholar
2.Feldman, N. I., Approximation of number π by algebraic numbers from special fields, J. Number Theory 9 (1977), 48–60.CrossRefGoogle Scholar