Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-12T01:46:34.452Z Has data issue: false hasContentIssue false
  • English
  • Français

On Schachermayer's example about the Banach-Saks property

Published online by Cambridge University Press:  18 May 2009

Carmelo Nunez
Carmelo Nunez
Affiliation:
Departamento De Analisis MatematicoFacultad De MatematicasUniversidad Complutense28040—Madrid, Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Banach space (X, ∥.∥) is said to have the Banach-Saks property (B.S.P.) if, for every bounded sequence (xn) in X, we can choose a subsequence (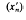) of (xn) such that the sequence

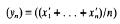
converges in the X-norm. This property, that a Banach space may enjoy or not, has been extensively studied.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 2 , May 1990 , pp. 201 - 203
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Beauzamy, B. and Lapreste, J. T., Modèles étaleś des espaces de Banach, (Hermann, Paris, 1984).Google Scholar
2.Bourgain, J., An averaging result for Co-sequences, Bull. Soc. Math. Belg. 30 (1978), 83–87.Google Scholar
3.Diestel, J. and Uhl, J. J. Jr, Vector measures, Surveys of the Amer. Math. Soc. 15, (A.M.S., 1977).CrossRefGoogle Scholar
4.Pisier, G., Une propriété de stabilité de la classe de spaces ne contenant pas I1, C.R. Acad. Sci. Paris. Sér, A 286 (1978), 747–749.Google Scholar
5.Rosenthal, H. P., Weakly independent sequences and the Banach-Saks property, Bull. London Math. Soc. 8 (1976), 22–24.Google Scholar
6.Schachermayer, W., A Banach space E such that L2(E) is not Banach-Saks, Israel J. Math. 40 (1981), 340–344.CrossRefGoogle Scholar
7.Talagrand, M., Weak Cauchy sequences in L1(E), Amer. J. Math. 106 (1984), 703–725.CrossRefGoogle Scholar