Article contents
On right duo p.p. rings
Published online by Cambridge University Press: 18 May 2009
Extract
Throughout the paper, rings are associative rings with identity. A ring is called right duo if every right ideal is two-sided, and it is called right p.p. if every principal right ideal is projective. A left duo (p.p.) ring is denned similarly, and a duo (p.p.) ring will mean a ring which is both right and left duo (p.p.). There is a right p.p. ring that is not left p.p. (see Chase [2[). Small [9] proved that right p.p. implies left p.p. if there are no infinite sets of orthogonal idempotents, and Endo [5, Proposition 2] has shown the same implication in the case where each idempotent in the ring is central. Since Courter [3, Theorem 1.3] noted that every idempotent in a right duo ring is central, we can simply speak of right duo p.p. rings. A typical example of a right duo ring which is not left duo is the following. Let F be a field and F(x) the field of rational functions over F. Let R = F(x)× F(x) as an additive group and define the multiplication as follows:
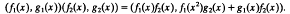
Then R is a local artinian ring with c(RR) = 2 and c(RR)= 3. Thus R is right duo but not left due.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1990
References
REFERENCES
- 15
- Cited by


