Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Faltings, Gerd
1987.
Hodge-tate structures and modular forms.
Mathematische Annalen,
Vol. 278,
Issue. 1-4,
p.
133.
Bayer, Pilar
and
González, Josep
1997.
On the Hasse–Witt Invariants of Modular Curves.
Experimental Mathematics,
Vol. 6,
Issue. 1,
p.
57.
Ochiai, Tadashi
2000.
Control Theorem for Bloch–Kato's Selmer Groups of p-Adic Representations.
Journal of Number Theory,
Vol. 82,
Issue. 1,
p.
69.
Dieulefait, Luis
and
Vila, Núria
2000.
Projective Linear Groups as Galois Groups overQvia Modular Representations.
Journal of Symbolic Computation,
Vol. 30,
Issue. 6,
p.
799.
Ochiai, Tadashi
2001.
Control Theorem for Greenberg's Selmer Groups of Galois Deformations.
Journal of Number Theory,
Vol. 88,
Issue. 1,
p.
59.
Dieulefait, Luis V.
2002.
Explicit Determination of the Images of the Galois Representations Attached to Abelian Surfaces with End(A) = Z.
Experimental Mathematics,
Vol. 11,
Issue. 4,
p.
503.
Dieulefait, Luis V.
2002.
On the images of the Galois representations attached to genus 2 Siegel modular forms.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2002,
Issue. 553,
Bruinier, Jan H.
and
Ono, Ken
2003.
Coefficients of half-integral weight modular forms.
Journal of Number Theory,
Vol. 99,
Issue. 1,
p.
164.
Iovita, Adrian
and
Spiess, Michael
2003.
Derivatives of p-adic L-functions, Heegner cycles and monodromy modules attached to modular forms.
Inventiones mathematicae,
Vol. 154,
Issue. 2,
p.
333.
Dieulefait, Luis V.
and
Rotger, Victor
2004.
The arithmetic of QM-abelian surfaces through their Galois representations.
Journal of Algebra,
Vol. 281,
Issue. 1,
p.
124.
Vila, Núria
2004.
Algebra, Arithmetic and Geometry with Applications.
p.
775.
Ahlgren, Scott
and
Boylan, Matthew
2005.
Coefficients of half-integral weight modular forms modulo ?j.
Mathematische Annalen,
Vol. 331,
Issue. 1,
p.
219.
Kiming, Ian
and
Verrill, Helena A.
2005.
On modular modℓ Galois representations with exceptional images.
Journal of Number Theory,
Vol. 110,
Issue. 2,
p.
236.
Dieulefait, Luis
and
Dimitrov, Mladen
2006.
Explicit determination of images of Galois representations attached to Hilbert modular forms.
Journal of Number Theory,
Vol. 117,
Issue. 2,
p.
397.
Virdol, Cristian
2006.
Zeta functions of twisted modular curves.
Journal of the Australian Mathematical Society,
Vol. 80,
Issue. 1,
p.
89.
Kumar Murty, V.
2007.
A variant of Lehmer's conjecture.
Journal of Number Theory,
Vol. 123,
Issue. 1,
p.
80.
Sorensen, Claus M.
2009.
Level-raising for Saito–Kurokawa forms.
Compositio Mathematica,
Vol. 145,
Issue. 4,
p.
915.
CHIDA, MASATAKA
2009.
INDIVISIBILITY OF ORDERS OF SELMER GROUPS FOR MODULAR FORMS.
International Journal of Number Theory,
Vol. 05,
Issue. 02,
p.
271.
Virdol, Cristian
2010.
On l-adic representations attached to Hilbert and Picard modular surfaces.
Journal of Number Theory,
Vol. 130,
Issue. 5,
p.
1197.
Dieulefait, L.
2010.
On the modularity of rigid Calabi−Yau threefolds: epilogue.
Journal of Mathematical Sciences,
Vol. 171,
Issue. 6,
p.
725.


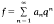 is a newform of weight
is a newform of weight 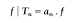
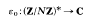
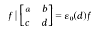
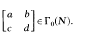 .
.