Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-26T02:59:49.387Z Has data issue: false hasContentIssue false
  • English
  • Français

On joint essential spectra of doubly commuting n-tuples of p-hyponormal operators

Published online by Cambridge University Press:  18 May 2009

In Ho Jeon
In Ho Jeon
Affiliation:
Department of Mathematics, Sung Kyun Kwan University, Suwon 440–746, South Korea, E-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be an operator on a Hillbert space with polar decomposition A = |A|, let  = |A|½U|A|½ and let  = V|Â| be the polar decomposition of Â. Write à for the operatorà = |Â|½V|Â|½. If 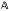= (A1,…,AN) is a doubly commuting n-tuple of p-hyponormal operators on a Hillbert space with equal defect and nullity, then 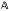= (Ã1,…,Ãn) is a doubly commuting n-tuple of hyponormal operators. In this paper we show that

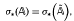
where σ* denotes σTe (Taylor essential spectrum), σTw (Taylor-Weyl spectrum) and σTb (Taylor-Browder spectrum), respectively.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 40 , Issue 3 , September 1998 , pp. 353 - 358
Copyright
Copyright © Glasgow Mathematical Journal Trust 1998

References

REFERENCES

1.Aluthge, A., On p-hyponormal operators for 0<p<1 Integral Equations Operator Theory 13 (1990), 307–315.CrossRefGoogle Scholar
2.Aluthge, A., Some generalized theorems on p-hyponormal operators, Integral Equations Operator Theory 24 (1996), 497–501.CrossRefGoogle Scholar
3.Chō, M., On the joint Weyl spectrum III, Ada Sci. Math. (Szeged) 53 (1992), 365–367.Google Scholar
4.Chō, M., Spectral properties of p-hyponormal operators, Glasgow Math. J. 36 (1994), 117–122.CrossRefGoogle Scholar
5.Curto, R. E., Fredholm and invertible n-tuples of operators. The deformation problem, Trans. Amer. Math. Soc. 266 (1981), 129–159.Google Scholar
6.Curto, R. E., Applications of several complex variables to multiparameter spectral theory, Surveys of Some Recent Results in Operator Theory, Vol. II, Pitman Research Notes in Math. Series No. 192 (Longman, 1988), 25–95.Google Scholar
7.Curto, R. E. and Dash, A. T., Browder spectral systems, Proc. Amer. Math. Soc. 103 (1988), 407–412.CrossRefGoogle Scholar
8.Dash, A. T., Joint essential spectra, Pacific J. Math. 64 (1976), 119–128.CrossRefGoogle Scholar
9.Duggal, B. P., On quasi-similar p-hyponormal operators, Integral Equations Operator Theory 26 (1996), 338–345.CrossRefGoogle Scholar
10.Duggal, B. P., On the spectrum of n-tuples of p-hyponormal operators, Glasgow Math. J. 40 (1998), 123–131.CrossRefGoogle Scholar
11.Jeon, I. H. and Lee, W. Y., On the Taylor-Weyl spectrum, Ada Sci. Math. (Szeged) 59 (1994), 187–193.Google Scholar
12.Taylor, J. L., A joint spectrum for several commuting operators, J. Fund. Anal. 6 (1970), 172–191.CrossRefGoogle Scholar
13.Taylor, J. L., The analytic functional calculus for several commuting operators, Ada Math. 125 (1970), 1–38.Google Scholar
14.Xia, D., Spectral theory of hyponormal operators (Birkhäuser, 1983).CrossRefGoogle Scholar