Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T05:11:35.805Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GENERALISED PRONORMAL SUBGROUPS OF FINITE GROUPS

Published online by Cambridge University Press:  22 August 2014

A. BALLESTER-BOLINCHES ,
J. C. BEIDLEMAN ,
A. D. FELDMAN  and
M. F. RAGLAND
A. BALLESTER-BOLINCHES
Affiliation:
Departament d'Àlgebra, Universitat de València, 46100 Burjassot, València, Spain e-mail: [email protected]
J. C. BEIDLEMAN
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, KY 40506-0027, USA e-mail: [email protected]
A. D. FELDMAN
Affiliation:
Department of Mathematics, Franklin and Marshall College, Lancaster, PA 17604-3003, USA e-mail: [email protected]
M. F. RAGLAND
Affiliation:
Department of Mathematics, Auburn University Montgomery, Montgomery, AL 36124-4023, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a formation 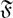$\mathfrak F$, a subgroup M of a finite group G is said to be 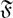$\mathfrak F$-pronormal in G if for each g ∈ G, there exists x ∈ 〈U,Ug〉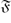$\mathfrak F$ such that Ux = Ug. Let f be a subgroup embedding functor such that f(G) contains the set of normal subgroups of G and is contained in the set of Sylow-permutable subgroups of G for every finite group G. Given such an f, let fT denote the class of finite groups in which f(G) is the set of subnormal subgroups of G; this is the class of all finite groups G in which to be in f(G) is a transitive relation in G. A subgroup M of a finite group G is said to be 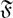$\mathfrak F$-normal in G if G/CoreG(M) belongs to 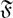$\mathfrak F$. A subgroup U of a finite group G is called K-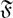$\mathfrak F$-subnormal in G if either U = G or there exist subgroups U = U0 ≤ U1 ≤ . . . ≤ Un = G such that Ui–1 is either normal or 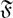$\mathfrak F$-normal in Ui, for i = 1,2, …, n. We call a finite group G an 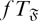$fT_{\mathfrak F}$-group if every K-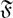$\mathfrak F$-subnormal subgroup of G is in f(G). In this paper, we analyse for certain formations 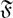$\mathfrak F$ the structure of 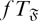$fT_{\mathfrak F}$-groups. We pay special attention to the 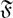$\mathfrak F$-pronormal subgroups in this analysis.

Keywords

20D1020D3520F17
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 56 , Issue 3 , September 2014 , pp. 691 - 703
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Ballester-Bolinches, A., Beidleman, J. C., Feldman, A. D. and Ragland, M. F., On generalised subnormal subgroups of finite groups, Math. Nachr. 286 (11–12) (2013), 1066–1071.Google Scholar
2.Ballester-Bolinches, A., Esteban-Romero, R. and Asaad, M., Products of finite groups, De Gruyter Expositions in Mathematics, vol. 53 (Springer, Berlin, Germany, 2010) 584 pp.Google Scholar
3.Ballester-Bolinches, A. and Ezquerro, L. M., Classes of finite groups, Mathematics and Its Applications (Springer, Berlin, Germany, 2006), 584 pp.Google Scholar
4.Ballester-Bolinches, A., Feldman, A. D., Pedraza-Aguilera, M. C. and Ragland, M. F., A class of generalised finite T-groups, J. Algebra 333 (1) (2011), 128–138.Google Scholar
5.Ballester-Bolinches, A. and Pérez-Ramos, M. D., On $\mathfrak F$-subnormal subgroups and Frattini-like subgroups of a finite group, Glasgow Math. J. 36 (1994), 241–247.Google Scholar
6.Beidleman, J. C. and Heineken, H., Finite soluble groups whose subnormal subgroups permute with certain classes of subgroups, J. Group Theory 6 (2003), 139–158.CrossRefGoogle Scholar
7.Bryce, R. A. and Cossey, J., The Wielandt subgroup of a finite soluble group, J. London Math. Soc. 40 (1989), 244–256.Google Scholar
8.Doerk, K. and Hawkes, T., Finite soluble groups (De Gruyter, Berlin, Germany, 1992).Google Scholar
9.Feldman, A., $\mathfrak F$-Bases and subgroup embedding in finite solvable groups, Arch. Math. 47 (1986), 481–492.CrossRefGoogle Scholar
10.Feldman, A. D., t-groups and their generalizations, Group theory (Granville, OH, 1992) (World Sci. Publ., River Edge, NJ, 1993), 128–133.Google Scholar
11.Müller, N., $\mathfrak F$-pronormale untergruppen endlich auflösbarer gruppen. (Johannes Gutenberg-Universität Mainz, Diplomarbeit, 1985).Google Scholar
12.Peng, T. A., Finite groups with pro-normal subgroups, Proc. Amer. Math. Soc. 20 (1969), 232–234.Google Scholar
13.Robinson, D. J. S.A note on finite groups in which normality is transitive, Proc. Amer. Math. Soc. 19 (1968), 933–937.CrossRefGoogle Scholar