Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DOLINKA, IGOR
2012.
ON FREE SPECTRA OF VARIETIES OF LOCALLY THRESHOLD TESTABLE SEMIGROUPS.
International Journal of Algebra and Computation,
Vol. 22,
Issue. 06,
p.
1250055.
HORVÁTH, GÁBOR
KÁTAI-URBÁN, KAMILLA
PACH, PÉTER PÁL
PLUHÁR, GABRIELLA
PONGRÁCZ, ANDRÁS
and
SZABÓ, CSABA
2012.
ON FREE ALGEBRAS IN VARIETIES GENERATED BY ITERATED SEMIDIRECT PRODUCTS OF SEMILATTICES.
International Journal of Algebra and Computation,
Vol. 22,
Issue. 07,
p.
1250063.
DOLINKA, IGOR
2012.
ON FREE SPECTRA OF A CLASS OF FINITE INVERSE MONOIDS.
Journal of the Australian Mathematical Society,
Vol. 93,
Issue. 3,
p.
225.
Dolinka, Igor
2012.
On free spectra of finite monoids from the pseudovariety DA.
Semigroup Forum,
Vol. 85,
Issue. 2,
p.
244.


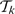 , the variety consisting of all
, the variety consisting of all 