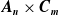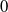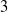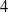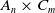1. Introduction
Understanding unramified extensions of number fields is of crucial importance in algebraic number theory, much like understanding the geometric fundamental groups of manifolds is in geometry.
In particular, a well-known open problem in number theory is the question whether, given any finite group
![]() $G$
, there exist infinitely many quadratic number fields possessing an everywhere unramified Galois extension with Galois group
$G$
, there exist infinitely many quadratic number fields possessing an everywhere unramified Galois extension with Galois group
![]() $G$
. It is furthermore of interest to determine explicit families of number fields having such an unramified extension. For the case of cyclic groups
$G$
. It is furthermore of interest to determine explicit families of number fields having such an unramified extension. For the case of cyclic groups
![]() $C_m$
, these questions are part of class field theory, and it has long been known that for any given integer
$C_m$
, these questions are part of class field theory, and it has long been known that for any given integer
![]() $n\gt 1$
, there exist infinitely many quadratic number fields such that the ideal class group has a cyclic subgroup of order
$n\gt 1$
, there exist infinitely many quadratic number fields such that the ideal class group has a cyclic subgroup of order
![]() $m$
(see [Reference Ankeny and Chowla1, Reference Nagell18, Reference Yamamoto23] for existence results as well as [Reference Gross and Rohrlich6, Reference Ito7, Reference Kishi9, Reference Louboutin14, Reference Murty16, Reference Murty17, Reference Soundararajan20, Reference Zhu and Wang24] for stronger quantitative as well as explicit computational results). See also the survey paper [Reference Bhand and Murty2]. On the other end of the scale is the case of non-abelian simple groups. The symmetric and alternating groups are among the relatively few groups for which the problem has been solved, and several previous results such as those of Uchida [Reference Uchida22], Yamamoto [Reference Yamamoto23], Elstrodt–Grunewald–Mennicke [Reference Elstrodt, Grunewald and Mennicke5], Kondo [Reference Kondo13], and Kedlaya [Reference Kedlaya8] are related to the existence of unramified extensions over quadratic fields whose Galois group is isomorphic to a symmetric or alternating group. Similar existence results for some other (small) nonabelian simple groups are contained in [Reference König, Neftin and Sonn12]. Going one step further, one may wish to investigate the problem for nonsolvable groups which are not generated by involutions, a condition that in practice tends to add to the difficulty, as explained in [Reference König10]. Some first results were obtained in [Reference König10] and [Reference König11], which solved the problem for certain nonsplit central extensions of simple groups such as
$m$
(see [Reference Ankeny and Chowla1, Reference Nagell18, Reference Yamamoto23] for existence results as well as [Reference Gross and Rohrlich6, Reference Ito7, Reference Kishi9, Reference Louboutin14, Reference Murty16, Reference Murty17, Reference Soundararajan20, Reference Zhu and Wang24] for stronger quantitative as well as explicit computational results). See also the survey paper [Reference Bhand and Murty2]. On the other end of the scale is the case of non-abelian simple groups. The symmetric and alternating groups are among the relatively few groups for which the problem has been solved, and several previous results such as those of Uchida [Reference Uchida22], Yamamoto [Reference Yamamoto23], Elstrodt–Grunewald–Mennicke [Reference Elstrodt, Grunewald and Mennicke5], Kondo [Reference Kondo13], and Kedlaya [Reference Kedlaya8] are related to the existence of unramified extensions over quadratic fields whose Galois group is isomorphic to a symmetric or alternating group. Similar existence results for some other (small) nonabelian simple groups are contained in [Reference König, Neftin and Sonn12]. Going one step further, one may wish to investigate the problem for nonsolvable groups which are not generated by involutions, a condition that in practice tends to add to the difficulty, as explained in [Reference König10]. Some first results were obtained in [Reference König10] and [Reference König11], which solved the problem for certain nonsplit central extensions of simple groups such as
![]() $\mathrm{SL}_2(\mathbb{F}_7)$
and
$\mathrm{SL}_2(\mathbb{F}_7)$
and
![]() $\mathrm{SL}_2(\mathbb{F}_5)$
.
$\mathrm{SL}_2(\mathbb{F}_5)$
.
In the same spirit, it is also natural to ask whether it is possible to find quadratic number fields having an
![]() $A_n$
-unramified extension and a
$A_n$
-unramified extension and a
![]() $C_m$
-unramified extension simultaneously. This is particularly interesting, since the solution requires to combine ideas from the realization of cyclic groups and simple groups, whose methods are otherwise often quite different. We give a partial answer to this question. Here is the main theorem.
$C_m$
-unramified extension simultaneously. This is particularly interesting, since the solution requires to combine ideas from the realization of cyclic groups and simple groups, whose methods are otherwise often quite different. We give a partial answer to this question. Here is the main theorem.
Main Theorem.
Let
![]() $n$
be an integer congruent to
$n$
be an integer congruent to
![]() $0$
(resp
$0$
(resp
![]() $3$
) modulo
$3$
) modulo
![]() $4$
and
$4$
and
![]() $m$
be an integer such that
$m$
be an integer such that
![]() $\gcd (n,m)=1$
(resp.
$\gcd (n,m)=1$
(resp.
![]() $\gcd (n-1,m)=1$
). If we assume that the ABC conjecture is true, then there exist infinitely many imaginary quadratic fields having an
$\gcd (n-1,m)=1$
). If we assume that the ABC conjecture is true, then there exist infinitely many imaginary quadratic fields having an
![]() $A_n \times C_m$
-unramified extension.
$A_n \times C_m$
-unramified extension.
The theorem will be proven in Section 3. The usefulness of the ABC conjecture to problems related to class number divisibility has been previously noticed by Murty, see [Reference Murty16]. Furthermore, the relevance of the ABC conjecture to counting squarefree discriminants of trinomials, and consequently to counting quadratic fields with unramified
![]() $A_n$
-extensions, was pointed out in [Reference Mukhopadhyay, Murty and Srinivas15]. It seems, however, that previously the two directions of “class number divisibility” and “unramified non-solvable (namely,
$A_n$
-extensions, was pointed out in [Reference Mukhopadhyay, Murty and Srinivas15]. It seems, however, that previously the two directions of “class number divisibility” and “unramified non-solvable (namely,
![]() $A_n$
)-extensions” have not been put together. The proof of our main theorem uses careful specialization of trinomial families to achieve these two goals simultaneously.
$A_n$
)-extensions” have not been put together. The proof of our main theorem uses careful specialization of trinomial families to achieve these two goals simultaneously.
In Section 4, we point out a special case in which the assertion follows unconditionally, without relying on the ABC conjecture.
2. Preliminaries
2.1. Trinomials and construction of
 $A_n$
-unramified extensions over quadratic fields
$A_n$
-unramified extensions over quadratic fields
There are several ways to construct
![]() $A_n$
-unramified extensions over quadratic fields. A well-known approach works with trinomials, that is, polynomials of the form
$A_n$
-unramified extensions over quadratic fields. A well-known approach works with trinomials, that is, polynomials of the form
![]() $X^n+aX^k+b$
. The following discriminant formula for trinomial extensions, due to Swan, will be very useful.
$X^n+aX^k+b$
. The following discriminant formula for trinomial extensions, due to Swan, will be very useful.
Theorem 2.1. (Theorem 2 of [Reference Swan21]): The trinomial
![]() $f(x)=X^n-aX^k+b$
with
$f(x)=X^n-aX^k+b$
with
![]() $0\lt k\lt n$
has discriminant:
$0\lt k\lt n$
has discriminant:
where
![]() $d=(n,k), N=n/d, K=k/d$
.
$d=(n,k), N=n/d, K=k/d$
.
Theorem 2.2. (Theorem 1 of [Reference Osada19]) Let
![]() $f(X) = X^n + aX^k+ b$
be a polynomial of rational integral coefficients, that is,
$f(X) = X^n + aX^k+ b$
be a polynomial of rational integral coefficients, that is,
![]() $f(X) \in \mathbb{Z}[X]$
. Let
$f(X) \in \mathbb{Z}[X]$
. Let
![]() $a = a_0c^n$
and
$a = a_0c^n$
and
![]() $b = b^k_0c^n$
. Then the Galois group of
$b = b^k_0c^n$
. Then the Galois group of
![]() $f$
is isomorphic to the symmetric group
$f$
is isomorphic to the symmetric group
![]() $S_n$
of degree
$S_n$
of degree
![]() $n$
if the following conditions are satisfied:
$n$
if the following conditions are satisfied:
-
1.
 $f(X)$
is irreducible ouer
$f(X)$
is irreducible ouer
 $\mathbb{Q}$
,
$\mathbb{Q}$
, -
2.
 $a_0c(n - k)k$
and
$a_0c(n - k)k$
and
 $nb_0$
are relatively prime, that is,
$nb_0$
are relatively prime, that is,
 $(a_0c(n - k)k,nb_0) = 1$
.
$(a_0c(n - k)k,nb_0) = 1$
.
Theorem 2.3. (Theorem 1 of [Reference Uchida22]) Let
![]() $k$
be an algebraic number field of finite degree. Let
$k$
be an algebraic number field of finite degree. Let
![]() $a$
and
$a$
and
![]() $b$
be integers of
$b$
be integers of
![]() $k$
. Let
$k$
. Let
and let
![]() $K$
denote the splitting field of
$K$
denote the splitting field of
![]() $f$
over
$f$
over
![]() $k$
, that is,
$k$
, that is,
![]() $K=k(\alpha _1, \alpha _2,\cdot \cdot \cdot,\alpha _n)$
where
$K=k(\alpha _1, \alpha _2,\cdot \cdot \cdot,\alpha _n)$
where
![]() $\alpha _1, \alpha _2,\cdot \cdot \cdot,\alpha _n)$
are the roots of
$\alpha _1, \alpha _2,\cdot \cdot \cdot,\alpha _n)$
are the roots of
![]() $f(X) = 0$
. Let
$f(X) = 0$
. Let
![]() $D$
be the discriminant of
$D$
be the discriminant of
![]() $f(X)$
. If
$f(X)$
. If
![]() $(n -1)a$
and
$(n -1)a$
and
![]() $nb$
are relatively prime,
$nb$
are relatively prime,
![]() $K$
is unramified over
$K$
is unramified over
![]() $k(\sqrt{D})$
.
$k(\sqrt{D})$
.
2.2. Divisibility of class numbers of imaginary quadratic fields
We collect some useful results on class number divisibility.
Proposition 2.4. (Proposition 1 of [Reference Soundararajan20]) Let
![]() $g \geq 3$
be an integer. Suppose that
$g \geq 3$
be an integer. Suppose that
![]() $d \geq 63$
is a squarefree integer such that
$d \geq 63$
is a squarefree integer such that
![]() $t^2d=m^g-n^2$
. Here,
$t^2d=m^g-n^2$
. Here,
![]() $t$
,
$t$
,
![]() $m$
, and
$m$
, and
![]() $n$
are positive integers with
$n$
are positive integers with
![]() $(m, 2n)=1$
and with
$(m, 2n)=1$
and with
![]() $m^g\lt (d+1)^2$
. Then,
$m^g\lt (d+1)^2$
. Then,
![]() $\mathrm{CL}({-}d)$
contains an element of order
$\mathrm{CL}({-}d)$
contains an element of order
![]() $g$
where
$g$
where
![]() $\mathrm{CL}({-}d)$
is the class group of
$\mathrm{CL}({-}d)$
is the class group of
![]() $\mathbb{Q}(\sqrt{-d})$
.
$\mathbb{Q}(\sqrt{-d})$
.
Notice the condition
![]() $m^g\lt (d+1)^2$
in the above proposition, which is exactly the reason why the ABC conjecture will be needed in our proof. There are also numerous results on class number divisibility of certain families of quadratic fields which do not require such extra conditions. Among those, the following is particularly well suited to our problem.
$m^g\lt (d+1)^2$
in the above proposition, which is exactly the reason why the ABC conjecture will be needed in our proof. There are also numerous results on class number divisibility of certain families of quadratic fields which do not require such extra conditions. Among those, the following is particularly well suited to our problem.
Theorem 2.5. (Main Theorem of [Reference Zhu and Wang24]) Let
![]() $k$
be an odd integer with
$k$
be an odd integer with
![]() $k\gt 1$
and
$k\gt 1$
and
![]() $2^{2m} \lt k^n$
where
$2^{2m} \lt k^n$
where
![]() $m$
is a positive integer and
$m$
is a positive integer and
![]() $n$
is an odd positive integer with
$n$
is an odd positive integer with
![]() $n\gt 3$
. Suppose that
$n\gt 3$
. Suppose that
![]() $2^{2m} - k^n \not \equiv 5$
(
$2^{2m} - k^n \not \equiv 5$
(
![]() $\mathrm{mod}$
$\mathrm{mod}$
![]() $8$
). Then the class group of the imaginary quadratic field
$8$
). Then the class group of the imaginary quadratic field
![]() $\mathbb{Q}(\sqrt{2^{2m} - k^n})$
contains an element of order
$\mathbb{Q}(\sqrt{2^{2m} - k^n})$
contains an element of order
![]() $n$
.
$n$
.
Remark 2.6.
Note that in [Reference Zhu and Wang24], the assumptions of the theorem are weaker; we only extracted the case relevant to our application. On the other hand, in [Reference Zhu and Wang24], the conclusion is worded only in terms of order of the class group, not in terms of order of elements. The latter is a priori stronger, but the proof in [Reference Zhu and Wang24] does indeed yield this stronger version. We briefly summarize the points relevant to this stronger conclusion. Let
![]() $-dy^2=2^{2m} - k^n$
where
$-dy^2=2^{2m} - k^n$
where
![]() $d$
is a squarefree integer. Then, we know that
$d$
is a squarefree integer. Then, we know that
![]() $2^{2m} +y^2d= k^n$
and
$2^{2m} +y^2d= k^n$
and
![]() $\left(2^{m}+y\sqrt{-d}\right)=\mathfrak{k}^n$
for some ideal
$\left(2^{m}+y\sqrt{-d}\right)=\mathfrak{k}^n$
for some ideal
![]() $\mathfrak{k}$
. We want to show that the ideal class of
$\mathfrak{k}$
. We want to show that the ideal class of
![]() $\mathfrak{k}$
has order
$\mathfrak{k}$
has order
![]() $n$
. To do this, one has to show that
$n$
. To do this, one has to show that
![]() $2^{m}+y\sqrt{-d} \neq \left(x_1+y_1\sqrt{-d}\right)^{t}$
for all divisors
$2^{m}+y\sqrt{-d} \neq \left(x_1+y_1\sqrt{-d}\right)^{t}$
for all divisors
![]() $t\ne 1$
of
$t\ne 1$
of
![]() $n$
.
$n$
.
![]() $\big($
If
$\big($
If
![]() $2^{m}+y\sqrt{-d} = \big(x_1+y_1\sqrt{-d}\big)^{t}$
for some
$2^{m}+y\sqrt{-d} = \big(x_1+y_1\sqrt{-d}\big)^{t}$
for some
![]() $t$
, then we know that the order of
$t$
, then we know that the order of
![]() $\mathfrak{k}$
is a divisor of
$\mathfrak{k}$
is a divisor of
![]() $n/t$
.
$n/t$
.
![]() $\big)$
$\big)$
Suppose that
![]() $2^{m}+y\sqrt{-d} = \left(x_1+y_1\sqrt{-d}\right)^{t}$
for some
$2^{m}+y\sqrt{-d} = \left(x_1+y_1\sqrt{-d}\right)^{t}$
for some
![]() $t$
. Then, [Reference Zhu and Wang24] deduces a contradiction unless
$t$
. Then, [Reference Zhu and Wang24] deduces a contradiction unless
![]() $t=3$
. If
$t=3$
. If
![]() $t=3$
, there is a contradiction when
$t=3$
, there is a contradiction when
![]() $2^{2m} - k^n \not \equiv 5$
(
$2^{2m} - k^n \not \equiv 5$
(
![]() $\mathrm{mod}$
$\mathrm{mod}$
![]() $8$
). (See the bottom of page 153 and the top of page 154 in [Reference Zhu and Wang24]
.) Thus,
$8$
). (See the bottom of page 153 and the top of page 154 in [Reference Zhu and Wang24]
.) Thus,
![]() $2^{m}+y\sqrt{-d} \neq \left(x_1+y_1\sqrt{-d}\right)^{t}$
for all
$2^{m}+y\sqrt{-d} \neq \left(x_1+y_1\sqrt{-d}\right)^{t}$
for all
![]() $t|n, t \neq 1$
when
$t|n, t \neq 1$
when
![]() $2^{2m} - k^n \not \equiv 5$
(
$2^{2m} - k^n \not \equiv 5$
(
![]() $\mathrm{mod}$
$\mathrm{mod}$
![]() $8$
). In other words, the order of
$8$
). In other words, the order of
![]() $\mathfrak{k}$
is
$\mathfrak{k}$
is
![]() $n$
and the class group of the ring of integer of
$n$
and the class group of the ring of integer of
![]() $\mathbb{Q}\left(\sqrt{2^{2m} - k^n}\right)$
has an element of order
$\mathbb{Q}\left(\sqrt{2^{2m} - k^n}\right)$
has an element of order
![]() $n$
.
$n$
.
2.3. The ABC conjecture
The ABC conjecture is stated in terms of three positive integers
![]() $a$
,
$a$
,
![]() $b$
, and
$b$
, and
![]() $c$
that are relatively prime and satisfy
$c$
that are relatively prime and satisfy
![]() $a + b = c$
. The conjecture essentially states that in this situation the radical of
$a + b = c$
. The conjecture essentially states that in this situation the radical of
![]() $abc$
, that is, the product of the distinct prime factors of
$abc$
, that is, the product of the distinct prime factors of
![]() $abc$
, cannot be too small. Here is the concrete statement.
$abc$
, cannot be too small. Here is the concrete statement.
The ABC Conjecture.
For each
![]() $\epsilon \gt 0$
, there are at most finitely many coprime triples
$\epsilon \gt 0$
, there are at most finitely many coprime triples
![]() $a, b, c$
of positive integers with
$a, b, c$
of positive integers with
![]() $a + b = c$
and
$a + b = c$
and
![]() $\mathrm{rad}(abc) \lt c^{1-\epsilon }$
. Here,
$\mathrm{rad}(abc) \lt c^{1-\epsilon }$
. Here,
![]() $\text{rad}(n)$
denotes the radical of a positive integer
$\text{rad}(n)$
denotes the radical of a positive integer
![]() $n$
.
$n$
.
3. Proof of the main theorem
We will now prove our main result.
Proof. Case 1:
![]() $n\equiv 3$
(mod
$n\equiv 3$
(mod
![]() $4$
). Let us consider the following polynomial:
$4$
). Let us consider the following polynomial:
where
![]() $k$
is an arbitrary integer. By Theorem 2.1, we know that the discriminant of
$k$
is an arbitrary integer. By Theorem 2.1, we know that the discriminant of
![]() $f(x)$
is
$f(x)$
is
Assume for the moment that
![]() $f$
is irreducible. Then the Galois group of the splitting field
$f$
is irreducible. Then the Galois group of the splitting field
![]() $K$
of
$K$
of
![]() $f$
is isomorphic to
$f$
is isomorphic to
![]() $S_n$
by Theorem 2.2. On the other hand, due to [Reference Dèbes4, Theorem 1.2], if the polynomial
$S_n$
by Theorem 2.2. On the other hand, due to [Reference Dèbes4, Theorem 1.2], if the polynomial
![]() $f$
is reducible for infinitely many choices of
$f$
is reducible for infinitely many choices of
![]() $k$
, then the two-variable polynomial
$k$
, then the two-variable polynomial
![]() $F(T,X) = X^n-X-n^uT^e$
must be reducible for some integer
$F(T,X) = X^n-X-n^uT^e$
must be reducible for some integer
![]() $u$
and positive integer
$u$
and positive integer
![]() $e$
. However, that polynomial is an Eisenstein polynomial in
$e$
. However, that polynomial is an Eisenstein polynomial in
![]() $T$
(for the prime
$T$
(for the prime
![]() $X$
of
$X$
of
![]() $\mathbb{Q}[X]$
) and therefore clearly irreducible. We have thus obtained that
$\mathbb{Q}[X]$
) and therefore clearly irreducible. We have thus obtained that
![]() $f$
has Galois group
$f$
has Galois group
![]() $S_n$
for all but finitely many choices of
$S_n$
for all but finitely many choices of
![]() $k$
. We also know that
$k$
. We also know that
![]() $K$
is unramified over
$K$
is unramified over
![]() $\mathbb{Q}\left(\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\right)$
, that is,
$\mathbb{Q}\left(\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\right)$
, that is,
![]() $\mathbb{Q}\left(\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\right)$
has an
$\mathbb{Q}\left(\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\right)$
has an
![]() $A_n$
-unramified extension
$A_n$
-unramified extension
![]() $K$
. The remaining task is to show that, for infinitely many choices of
$K$
. The remaining task is to show that, for infinitely many choices of
![]() $k$
, the class group of
$k$
, the class group of
![]() $\mathbb{Q}\left(\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\right)$
contains an element of
$\mathbb{Q}\left(\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\right)$
contains an element of
![]() $m$
. The discriminant of
$m$
. The discriminant of
![]() $f(x)$
can be written as follows:
$f(x)$
can be written as follows:
Here,
![]() $D$
is a squarefree integer. Set
$D$
is a squarefree integer. Set
![]() $A:=(n-1)^{n-1}$
,
$A:=(n-1)^{n-1}$
,
![]() $B=b^2D$
and
$B=b^2D$
and
![]() $C:=n^{n+k(n-1)}$
so that
$C:=n^{n+k(n-1)}$
so that
![]() $A+B=C$
. By Proposition 2.4, it suffices to show that
$A+B=C$
. By Proposition 2.4, it suffices to show that
![]() $(D+1)^2\gt C$
. If we assume the ABC conjecture, for a given
$(D+1)^2\gt C$
. If we assume the ABC conjecture, for a given
![]() $\epsilon \gt 0$
, for all but finitely many
$\epsilon \gt 0$
, for all but finitely many
![]() $(A,B,C)$
of this kind, one has
$(A,B,C)$
of this kind, one has
![]() $\mathrm{rad}(ABC) \gt C^{1-\epsilon }$
. From now on, we will write
$\mathrm{rad}(ABC) \gt C^{1-\epsilon }$
. From now on, we will write
![]() $a:=n+k(n-1)$
. We easily see that
$a:=n+k(n-1)$
. We easily see that
In other words,
As soon as
![]() $a\gt 8$
, one has
$a\gt 8$
, one has
![]() $\mathrm{rad}(B)\gt B^{3/4}$
. This means that
$\mathrm{rad}(B)\gt B^{3/4}$
. This means that
where
![]() $e_p$
is the multiplicity of
$e_p$
is the multiplicity of
![]() $p$
in the prime factorization of
$p$
in the prime factorization of
![]() $B$
. Since all the primes contributing to
$B$
. Since all the primes contributing to
![]() $b^2$
must divide
$b^2$
must divide
![]() $B$
more than once, it follows that the term
$B$
more than once, it follows that the term
![]() $b^2$
in the expression
$b^2$
in the expression
![]() $B=b^2D$
must be smaller than
$B=b^2D$
must be smaller than
![]() $(B^{1/4})^2 = B^{1/2}$
. Therefore, we know that
$(B^{1/4})^2 = B^{1/2}$
. Therefore, we know that
![]() $B=b^2D\lt B^{1/2}D$
and
$B=b^2D\lt B^{1/2}D$
and
![]() $B\lt D^2$
. Since
$B\lt D^2$
. Since
![]() $A$
is a fixed value (not depending on
$A$
is a fixed value (not depending on
![]() $k$
), if
$k$
), if
![]() $a$
is sufficiently large, we obtain the condition
$a$
is sufficiently large, we obtain the condition
![]() $A\lt B^{1/2}$
. In conclusion,
$A\lt B^{1/2}$
. In conclusion,
Since
![]() $n-1$
is relatively prime to
$n-1$
is relatively prime to
![]() $m$
, we can find positive integers
$m$
, we can find positive integers
![]() $k$
such that
$k$
such that
![]() $m| \big (n+k(n-1)\big )$
. Therefore, if we choose
$m| \big (n+k(n-1)\big )$
. Therefore, if we choose
![]() $k$
satisfying
$k$
satisfying
![]() $m| (n+k(n-1))$
and
$m| (n+k(n-1))$
and
![]() $n+k(n-1)=a\gt 8$
, the class group of
$n+k(n-1)=a\gt 8$
, the class group of
![]() $\mathbb{Q}\big (\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\big )$
contains an element of order
$\mathbb{Q}\big (\sqrt{(n-1)^{n-1}-n^{n+k(n-1)}}\big )$
contains an element of order
![]() $m$
under the assumption of the ABC conjecture.
$m$
under the assumption of the ABC conjecture.
Case 2:
![]() $n\equiv 0$
(mod
$n\equiv 0$
(mod
![]() $4$
). Let us consider the polynomial:
$4$
). Let us consider the polynomial:
where
![]() $k$
is an arbitrary integer. We know that the discriminant of
$k$
is an arbitrary integer. We know that the discriminant of
![]() $f(X)$
is
$f(X)$
is
By an argument analogous to the above, we know that
![]() $f$
has Galois group
$f$
has Galois group
![]() $S_n$
and the splitting field
$S_n$
and the splitting field
![]() $K$
of
$K$
of
![]() $f$
is unramified over
$f$
is unramified over
![]() $\mathbb{Q}\left(\sqrt{n^{n}-(n-1)^{n-1+nk}}\right)$
for all but finitely many choices of
$\mathbb{Q}\left(\sqrt{n^{n}-(n-1)^{n-1+nk}}\right)$
for all but finitely many choices of
![]() $k$
. We also want to show that
$k$
. We also want to show that
![]() $\mathbb{Q}\left(\sqrt{n^{n}-(n-1)^{n-1+nk}}\right)$
has a
$\mathbb{Q}\left(\sqrt{n^{n}-(n-1)^{n-1+nk}}\right)$
has a
![]() $C_m$
-unramified extension by the similar way. The discriminant of
$C_m$
-unramified extension by the similar way. The discriminant of
![]() $f(x)$
can be written as follows:
$f(x)$
can be written as follows:
where
![]() $D$
is a squarefree integer. Set
$D$
is a squarefree integer. Set
![]() $A:=n^n$
,
$A:=n^n$
,
![]() $B:=b^2D$
, and
$B:=b^2D$
, and
![]() $C:=(n-1)^{n-1+nk}$
so that
$C:=(n-1)^{n-1+nk}$
so that
![]() $A+B=C$
. By the similar argument in the above, under the assumption of the ABC conjecture, for a given
$A+B=C$
. By the similar argument in the above, under the assumption of the ABC conjecture, for a given
![]() $\epsilon \gt 0$
, for all but finitely many
$\epsilon \gt 0$
, for all but finitely many
![]() $(A,B,C)$
, we have
$(A,B,C)$
, we have
![]() $\mathrm{rad}(ABC) \gt C^{1-\epsilon }$
. Set
$\mathrm{rad}(ABC) \gt C^{1-\epsilon }$
. Set
![]() $a=n(k+1)-1$
. We know that
$a=n(k+1)-1$
. We know that
It means that,
In particular, for
![]() $a\gt 12$
, we have
$a\gt 12$
, we have
![]() $\mathrm{rad}(B)\gt B^{3/4}$
. This implies that
$\mathrm{rad}(B)\gt B^{3/4}$
. This implies that
With the same development as in Case 1, we can deduce
for all sufficiently large
![]() $a$
. With the same idea as in Case 1, if we put
$a$
. With the same idea as in Case 1, if we put
![]() $k$
satisfying
$k$
satisfying
![]() $m| (n-1+nk)$
(which is possible since
$m| (n-1+nk)$
(which is possible since
![]() $m$
and
$m$
and
![]() $n$
are coprime) and
$n$
are coprime) and
![]() $n-1+kn=a\gt 12$
, the class group of
$n-1+kn=a\gt 12$
, the class group of
![]() $\mathbb{Q}\big (\sqrt{n^{n}-(n-1)^{n-1+kn}}\big )$
contains an element of order
$\mathbb{Q}\big (\sqrt{n^{n}-(n-1)^{n-1+kn}}\big )$
contains an element of order
![]() $m$
under the assumption of the ABC conjecture.
$m$
under the assumption of the ABC conjecture.
4. An unconditional result
Although we have proven our Main Theorem under the assumption of the ABC conjecture, in special cases, it is possible to prove it without this assumption. We will explain such a case in this section.
Theorem 4.1.
Let
![]() $n=2^\ell$
be a
$n=2^\ell$
be a
![]() $2$
-power. Then there exist infinitely many imaginary quadratic fields having an
$2$
-power. Then there exist infinitely many imaginary quadratic fields having an
![]() $A_{n} \times C_m$
-unramified extension where
$A_{n} \times C_m$
-unramified extension where
![]() $m$
is any odd integer.
$m$
is any odd integer.
Table 1. Numerical examples for
![]() $n=7,8,11,12,15,16$
$n=7,8,11,12,15,16$

Proof. Let us again consider the following polynomial:
We know that the discriminant of
![]() $f$
is of the form:
$f$
is of the form:
As we have already seen in the proof of the previous theorem,
![]() $f(x)$
is irreducible and the Galois group of the splitting field
$f(x)$
is irreducible and the Galois group of the splitting field
![]() $K$
of
$K$
of
![]() $f$
is isomorphic to
$f$
is isomorphic to
![]() $S_n$
for all but finitely many choices of
$S_n$
for all but finitely many choices of
![]() $k$
. By Theorem 2.3, we also know that
$k$
. By Theorem 2.3, we also know that
![]() $K$
is unramified over
$K$
is unramified over
![]() $\mathbb{Q}\left(\sqrt{2^{n\ell }-(n-1)^{n-1+nk}}\right)$
. Since
$\mathbb{Q}\left(\sqrt{2^{n\ell }-(n-1)^{n-1+nk}}\right)$
. Since
![]() $m$
is an odd integer, we can find (infinitely many)
$m$
is an odd integer, we can find (infinitely many)
![]() $k$
such that
$k$
such that
![]() $m | \big (n-1+nk\big )$
. Since
$m | \big (n-1+nk\big )$
. Since
![]() $n=2^{\ell }$
and
$n=2^{\ell }$
and
![]() $n-1+nk$
is an odd integer, we know that
$n-1+nk$
is an odd integer, we know that
![]() $2^{n\ell }-(n-1)^{n-1+nk} \equiv 1$
(
$2^{n\ell }-(n-1)^{n-1+nk} \equiv 1$
(
![]() $\mathrm{mod}$
$\mathrm{mod}$
![]() $8$
). By Theorem 2.5, the class group of the imaginary quadratic field
$8$
). By Theorem 2.5, the class group of the imaginary quadratic field
![]() $\mathbb{Q}\left(\sqrt{2^{n\ell }-(n-1)^{n-1+nk}}\right)$
contains an element of order
$\mathbb{Q}\left(\sqrt{2^{n\ell }-(n-1)^{n-1+nk}}\right)$
contains an element of order
![]() $n-1+nk$
, and hence one of order
$n-1+nk$
, and hence one of order
![]() $m$
.
$m$
.
5. Numerical examples
In this section, we will give several explicit examples of quadratic fields with
![]() $A_n\times C_m$
-unramified extensions illustrating the proof of the Main Theorem. All computations in this section were carried out with Magma (see [Reference Bosma, Cannon and Playoust3]). The contents of Table 1 are described as follows (with the two cases depending on the mod-
$A_n\times C_m$
-unramified extensions illustrating the proof of the Main Theorem. All computations in this section were carried out with Magma (see [Reference Bosma, Cannon and Playoust3]). The contents of Table 1 are described as follows (with the two cases depending on the mod-
![]() $4$
residue of
$4$
residue of
![]() $n$
):
$n$
):
![]() $n$
: an integer congruent to
$n$
: an integer congruent to
![]() $3$
(resp.
$3$
(resp.
![]() $0$
) modulo
$0$
) modulo
![]() $4$
,
$4$
,
![]() $k$
: an auxiliary integer,
$k$
: an auxiliary integer,
![]() $m$
: the integer
$m$
: the integer
![]() $m= n+k(n-1)$
(resp.
$m= n+k(n-1)$
(resp.
![]() $m= n-1+nk$
),
$m= n-1+nk$
),
![]() $f(x)$
: the polynomial
$f(x)$
: the polynomial
![]() $f(x)=x^n-x-n^k$
(resp.
$f(x)=x^n-x-n^k$
(resp.
![]() $f(x)=x^n-(n-1)^kx+1$
),
$f(x)=x^n-(n-1)^kx+1$
),
![]() $K$
: the splitting field of
$K$
: the splitting field of
![]() $f(x)$
,
$f(x)$
,
![]() $-d$
: the squarefree part of the discriminant of
$-d$
: the squarefree part of the discriminant of
![]() $f(x)$
.
$f(x)$
.
Acknowledgments
The first author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2021R1F1A1054926). The second author was supported by the National Research Foundation of Korea (NRF Basic Research Grant RS-2023-00239917).