Article contents
ON ANNIHILATOR IDEALS OF SKEW MONOID RINGS*
Published online by Cambridge University Press: 04 December 2009
Abstract
A ring R is called a left APP-ring if the left annihilator lR(Ra) is pure as a left ideal of R for every a ∈ R; R is called (left principally) quasi-Baer if the left annihilator of every (principal) left ideal of R is generated by an idempotent. Let R be a ring and M an ordered monoid. Assume that there is a monoid homomorphism φ: M ⟶ Aut(R). We give a necessary and sufficient condition for the skew monoid ring 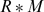 (induced by φ) to be left APP (left principally quasi-Baer, quasi-Baer, respectively).
(induced by φ) to be left APP (left principally quasi-Baer, quasi-Baer, respectively).
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2009
References
REFERENCES
- 4
- Cited by


