Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T01:00:27.226Z Has data issue: false hasContentIssue false
  • English
  • Français

On an integral equation of Šub-Sizonenko

Published online by Cambridge University Press:  18 May 2009

P. G. Rooney
P. G. Rooney
Affiliation:
University of Toronto, Toronto, Canada, M5S 1A1.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The integral equation of the title is

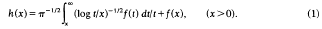
It was studied in [4], though h(x) was written as x-1g(x-1) there, and using a method involving orthogonal Watson transformations, it was shown there that if h ∈ L2(0, ∞), then the equation has a solution f ∈ L2(0, ∞), and that / is given by

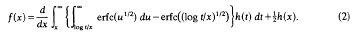
In this paper, using the techniques of [3], we shall show that the equation can be solved for ℎ in the space ℒμ, p of [3] for 1 ≤ p < ∘, μ > 0, and that for these spaces, which include L2(0, ∘), f is given by the simpler formula

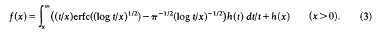
We shall further show that these results can be extended to the spaces ℒw, μ, p of [3]. This forms the content of our theorem below.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 2 , July 1983 , pp. 207 - 210
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Erdélyi, A. et al. , Tables of integral transforms I, (McGraw-Hill, 1954).Google Scholar
2.Rooney, P. G., On the ranges of certain fractional integrals, Canad. J. Math. 24 (1952), 1198–1216.CrossRefGoogle Scholar
3.Rooney, P. G., Multipliers for the Mellin transformation, Canad. Math. Bull, (to appear).Google Scholar
4.Šub-Sizonenko, J. A., Inversion of an integral operator by the method of expansion with respect to orthogonal Watson operators, Siberian Math. J. 20 (1979), 318–321. (Also Sibirsk. Mat. Ž. 20 (1979), 445–448.)CrossRefGoogle Scholar