Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T08:18:20.799Z Has data issue: false hasContentIssue false
  • English
  • Français

ON AN EIGENVALUE PROBLEM FOR AN ANISOTROPIC ELLIPTIC EQUATION INVOLVING VARIABLE EXPONENTS

Published online by Cambridge University Press:  25 August 2010

MIHAI MIHĂILESCU  and
GHEORGHE MOROŞANU
MIHAI MIHĂILESCU
Affiliation:
Department of Mathematics, Central European University, 1051 Budapest, Hungary Department of Mathematics, University of Craiova, 200585 Craiova, Romania e-mail: [email protected]
GHEORGHE MOROŞANU
Affiliation:
Department of Mathematics, Central European University, 1051 Budapest, Hungary e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

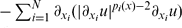We study the eigenvalue problem = λ|u|q(x)−2u in Ω, u = 0 on ∂Ω, where Ω is a bounded domain in ℝN with smooth boundary ∂Ω, λ is a positive real number, and p1,⋅ ⋅ ⋅, pN, q are continuous functions satisfying the following conditions: 2 ≤ pi(x) < N, 1 < q(x) for all x ∈ Ω, i ∈ {1,. . .,N}; there exist j, k ∈ {1,. . .,N}, j ≠ k, such that pj ≡ q in Ω, q is independent of xj and maxΩq < minΩpk. The main result of this paper establishes the existence of two positive constants λ0 and λ1 with λ0 ≤ λ1 such that every λ ∈(λ1, ∞) is an eigenvalue, while no λ ∈ (0, λ0) can be an eigenvalue of the above problem.

Keywords

35D0535J6035J7058E05
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 3 , September 2010 , pp. 517 - 527
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Acerbi, E. and Mingione, G., Regularity results for a class of functionals with nonstandard growth, Arch. Ration. Mech. Anal. 156 (2001), 121–140.Google Scholar
2.Acerbi, E. and Mingione, G., Gradient estimates for the p(x)–Laplacean system, J. Reine Angew. Math. 584 (2005), 117–148.CrossRefGoogle Scholar
3.Alves, C. O. and Souto, M. A., Existence of solutions for a class of problems in ℝN involving the p(x)–Laplacian, in Contributions to nonlinear analysis, a tribute to D.G. de Figueiredo on the occasion of his 70th birthday (Cazenave, T., Costa, D., Lopes, O., Manàsevich, R., Rabinowitz, R., Ruf, R. and Tomei, C., Editors), Progress in Nonlinear Differential Equations and Their Applications, Vol. 66 (Birkhäuser, Basel, Switzerland, 2006), 17–32.Google Scholar
4.Anane, A., Simplicité et isolation de la première valeur propre du p-laplacien avec poids, C. R. Acad. Sci. Paris Sér. I 305 (1987), 725–728.Google Scholar
5.Chabrowski, J. and Fu, Y., Existence of solutions for p(x)–Laplacian problems on a bounded domain, J. Math. Anal. Appl. 306 (2005), 604–618.CrossRefGoogle Scholar
6.Chen, Y., Levine, S. and Rao, M., Variable exponent, linear growth functionals in image processing, SIAM J. Appl. Math. 66 (2006), 1383–1406.Google Scholar
7.Diening, L., Theoretical and numerical results for electrorheological fluids, PhD thesis (University of Frieburg, Germany, 2002).Google Scholar
8.Edmunds, D. E., Lang, J. and Nekvinda, A., On Lp(x) norms, Proc. R. Soc. Lond. Ser. A 455 (1999), 219–225.CrossRefGoogle Scholar
9.Edmunds, D. E. and Rákosník, J., Density of smooth functions in Wk,p(x)(Ω), Proc. R. Soc. Lond. Ser. A 437 (1992), 229–236.Google Scholar
10.Edmunds, D. E. and Rákosník, J., Sobolev embedding with variable exponent, Studia Math. 143 (2000), 267–293.CrossRefGoogle Scholar
11.Fan, X., Remarks on eigenvalue problems involving the p(x)-Laplacian, J. Math. Anal. Appl. 352 (2009), 85–98.CrossRefGoogle Scholar
12.Fan, X., Zhang, Q. and Zhao, D., Eigenvalues of p(x)-Laplacian Dirichlet problem, J. Math. Anal. Appl. 302 (2005), 306–317.CrossRefGoogle Scholar
13.Fragalà, I., Gazzola, F. and Kawohl, B., Existence and nonexistence results for anisotropic quasilinear equations, Ann. Inst. H. Poincaré, Anal. Non Linéaire 21 (2004), 715–734.CrossRefGoogle Scholar
14.Halsey, T. C., Electrorheological fluids, Science 258 (1992), 761–766.CrossRefGoogle ScholarPubMed
15.Harjulehto, P., Hästö, P., Koskenoja, M. and Varonen, S., The Dirichlet energy integral and variable exponent Sobolev spaces with zero boundary values, Potential Anal. 25 (2006), 79–94.CrossRefGoogle Scholar
16.Hästö, P., On the density of continuous functions in variable exponent Sobolev spaces, Rev. Mat. Iberoamericana 23 (2007), 74–82.CrossRefGoogle Scholar
17.Kováčik, O. and Rákosník, J., On spaces Lp(x) and W 1,p(x), Czech. Math. J. 41 (1991), 592–618.CrossRefGoogle Scholar
18.Mihăilescu, M. and Moroşanu, G., Existence and multiplicity of solutions for an anisotropic elliptic problem involving variable exponent growth conditions, Appl. Anal. 89 (2010), 257–271.CrossRefGoogle Scholar
19.Mihăilescu, M., Pucci, P. and Rădulescu, V., Eigenvalue problems for anisotropic quasilinear elliptic equations with variable exponent, J. Math. Anal. Appl. 340 (2008), 687–698.CrossRefGoogle Scholar
20.Mihăilescu, M. and Rădulescu, V., A multiplicity result for a nonlinear degenerate problem arising in the theory of electrorheological fluids, Proc. R. Soc. Lond. Ser. A 462 (2006), 2625–2641.Google Scholar
21.Mihăilescu, M. and Rădulescu, V., On a nonhomogeneous quasilinear eigenvalue problem in Sobolev spaces with variable exponent, Proc. Amer. Math. Soc. 135 (2007), 2929–2937.CrossRefGoogle Scholar
22.Mihăilescu, M. and Rădulescu, V., Continuous spectrum for a class of nonhomogeneous differential operators, Manuscr. Math. 125 (2008), 157–167.CrossRefGoogle Scholar
23.Mihăilescu, M. and Rădulescu, V., Spectrum in an unbounded interval for a class of nonhomogeneous differential operators, Bull. Lond. Math. Soc. 40 (6) (2008), 972–984.CrossRefGoogle Scholar
24.Musielak, J., Orlicz spaces and modular spaces, Lecture Notes in Mathematics, vol. 1034 (Springer, Berlin, 1983).CrossRefGoogle Scholar
25.Nikol'skii, S. M., On imbedding, continuation and approximation theorems for differentiable functions of several variables, Russ. Math. Surv. 16 (1961), 55–104.CrossRefGoogle Scholar
26.Pfeiffer, C., Mavroidis, C., Bar–Cohen, Y. and Dolgin, B., Electrorheological fluid based force feedback device, in Proc. 1999 SPIE Telemanipulator and Telepresence Technologies VI Conf., vol. 3840 (Boston, MA, 1999), pp. 88–99.CrossRefGoogle Scholar
27.Rákosník, J., Some remarks to anisotropic Sobolev spaces I, Beitr. Anal. 13 (1979), 55–68.Google Scholar
28.Rákosník, J., Some remarks to anisotropic Sobolev spaces II, Beitr. Anal. 15 (1981), 127–140.Google Scholar
29.Rajagopal, K. R. and Ruzicka, M., Mathematical modelling of electrorheological fluids, Contin. Mech. Thermodyn. 13 (2001), 59–78.CrossRefGoogle Scholar
30.Ruzicka, M., Electrorheological fluids: Modeling and mathematical theory (Springer–Verlag, Berlin, 2002).Google Scholar
31.Samko, S. and Vakulov, B., Weighted Sobolev theorem with variable exponent for spatial and spherical potential operators, J. Math. Anal. Appl. 310 (2005), 229–246.CrossRefGoogle Scholar
32.Struwe, M., Variational methods: Applications to nonlinear partial differential equations and Hamiltonian systems (Springer, Heidelberg, 1996).CrossRefGoogle Scholar
33.Troisi, M., Teoremi di inclusione per spazi di Sobolev non isotropi, Ricerche Mat. 18 (1969), 3–24.Google Scholar
34.Ven'–tuan, L., On embedding theorems for spaces of functions with partial derivatives of various degree of summability, Vestn. Leningr. Univ. 16 (1961), 23–37.Google Scholar
35.Zhikov, V., Averaging of functionals of the calculus of variations and elasticity theory, Math. USSR Izv. 29 (1987), 33–66.CrossRefGoogle Scholar