Article contents
Numerical ranges of powers of hermitian elements
Published online by Cambridge University Press: 18 May 2009
Extract
An element k of a unital Banach algebra A is said to be Hermitian if its numerical range
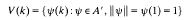
is contained in ℝ; equivalently, ∥eitk∥ = 1(t ∈ ℝ)—see Bonsall and Duncan [3] and [4]. Here we find the largest possible extent of V(kn), n ∈ ℕ, given V(k) ⊆ [−1, 1], and so ∥k∥ ≤ 1: previous knowledge is in Bollobás [2] and Crabb, Duncan and McGregor [7]. The largest possible sets all occur in a single example. Surprisingly, they all have straight line segments in their boundaries. The example is in [2] and [7], but here we give A. Browder's construction from [5], partly published in [6]. We are grateful to him for a copy of [5], and for discussions which led to the present work. We are also grateful to J. Duncan for useful discussions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1986
References
REFERENCES
- 1
- Cited by


