Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T07:35:03.878Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the modulus of convexity

Published online by Cambridge University Press:  18 May 2009

Andrew T. Plant
Andrew T. Plant
Affiliation:
Department of Mathematics, University Gardens, Glasgow, G12 8Qw
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1, Corollary 5], Figiel gives an elegant demonstration that the modulus ofconvexity δ in real Banach space X is nondecreasing, where

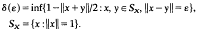
It is deduced from this that in fact δ(ɛ)/ɛ is nondecreasing [Proposition 3]. During the course of the proof [Lemma 4] it is stated that if v ∊ Sx is a local maximum on Sx of φ ∈Sx*, then v is a global maximum (φ(v) = 1). This is false; it could be that v is a global minimum. It is easy to construct such an example in R2 endowed with the maximum norm. What is true is that v is a global maximum of |φ|.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 22 , Issue 2 , July 1981 , pp. 157 - 158
Copyright
Copyright © Glasgow Mathematical Journal Trust 1981

References

REFERENCE

1.Figiel, T., On the moduli of convexity and smoothness, Studia Math.. 56 (1976), 121–155.CrossRefGoogle Scholar