Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T08:18:18.118Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON SOME TOPOLOGICAL PROPERTIES OF SETS WITH FINITE PERIMETER

Part of: Classical measure theory

Published online by Cambridge University Press:  23 July 2015

SILVANO DELLADIO
SILVANO DELLADIO*
Affiliation:
University of Trento, Department of Mathematics, via Sommarive 14, 38123 Trento, Italy e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

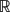Some well-known results about the 2-density topology on ${\mathcal R}$ (in particular in the context of the Lusin–Menchoff property) are extended to τbm , i.e. the m-density topology on 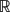${\mathcal R}$ n with m ∈ (n,+∞). Every set of finite perimeter in 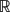${\mathcal R}$ n is equivalent (in measure) to a set in τb m 0 , where m 0=n+1+ 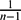${1\over n-1}$ . There exists a set of finite perimeter in ${\mathcal R}$ n which is not equivalent (in measure) to any member in the a.e.-modification of τbm , whatever m ∈ [n,+∞).

MSC classification

Primary: 28A75: Length, area, volume, other geometric measure theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 3 , September 2016 , pp. 637 - 647
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1. Alberti, G., A Lusin type theorem for gradients, J. Funct. Anal. 100 (1) (1991), 110–118.Google Scholar
2. Ambrosio, L., Caselles, V., Masnou, S. and Morel, J.-M., Connected components of sets of finite perimeter and applications to image processing, J. Eur. Math. Soc. 3 (1) (2001), 39–92.CrossRefGoogle Scholar
3. Ambrosio, L., Fusco, N. and Pallara, D., Functions of bounded variation and free discontinuity problems, Oxford Mathematical Monographs (Oxford University Press Inc., Oxford, UK, 2000).CrossRefGoogle Scholar
4. Caraballo, D. G., B2-convexity implies strong and weak lower semicontinuity of partitions of ${\mathcal R}$ n , Pac. J. Math. 253 (2) (2011), 321–348.CrossRefGoogle Scholar
5. Delladio, S., Functions of class C1 subject to a Legendre condition in an enhanced density set, Rev. Matem. Iberoam. 28 (1) (2012), 127–140.Google Scholar
6. Delladio, S., A short note on enhanced density sets, Glasgow Math. J. 53 (3) (2011), 631–635.Google Scholar
7. Delladio, S., A Whitney-type result about rectifiability of graphs, Riv. Mat. Univ. Parma 5 (2) (2014), 387–397.Google Scholar
8. Delladio, S., Some new results about the geometry of sets of finite perimeter, To appear on Proc. R. Soc. Edinburgh.Google Scholar
9. Dolzmann, G. and Müller, S., Microstructures with finite surface energy: The two-well problem, Arch. Rational Mech. Anal. 132 (2) (1995), 101–141.CrossRefGoogle Scholar
10. Figalli, A. and Maggi, F., On the shape of liquid drops and crystals in the small mass regime, Arch. Ration. Mech. Anal. 201 (1) (2011), 143–207.Google Scholar
11. Figalli, A., Maggi, F. and Pratelli, A., A mass transportation approach to quantitative isoperimetric inequalities, Invent. Math. 182 (1) (2010), 167–211.CrossRefGoogle Scholar
12. Fu, J. H. G., Erratum to “Some remarks on Legendrian rectifiable currents”, Manuscr. Math. 113 (3) (2004), 397–401.CrossRefGoogle Scholar
13. Gousseau, Y. and Morel, J.-M., Are natural images of bounded variation? SIAM J. Math. Anal. 33 (3) (2001), 634–648.CrossRefGoogle Scholar
14. Kirchheim, B., Lipschitz minimizers of the 3-well problem having gradients of bounded variation, Preprint 12, (Max Planck Institute for Mathematics in the Sciences, Leipzig, 1998).Google Scholar
15. Lukes, J., Maly, J. and Zajicek, L., Fine topology methods in real analysis and potential theory, Lect. Notes in Math., vol. 1189 (Springer Verlag, Berlin, Heidelberg, Germany, 1986).Google Scholar
16. Pavlica, D. and ZajÈek, L., Morse-Sard theorem for d.c. functions and mappings on ${\mathcal R}$ 2 , Indiana Univ. Math. J. 55 (3) (2006), 1195–1207.CrossRefGoogle Scholar