Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T16:56:05.836Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON p-CENTRAL GROUPS

Published online by Cambridge University Press:  25 February 2013

RACHEL CAMINA  and
ANITHA THILLAISUNDARAM
RACHEL CAMINA
Affiliation:
Fitzwilliam College, Cambridge, CB3 0DG, UK e-mail: [email protected]
ANITHA THILLAISUNDARAM
Affiliation:
Magdalene College, Cambridge, CB3 0AG, UK e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A group G is n-central if Gn ≤ Z(G), that is the subgroup of G generated by n-powers of G lies in the centre of G. We investigate pk-central groups for p a prime number. For G a finite group of exponent pk, the covering group of G is pk-central. Using this we show that the exponent of the Schur multiplier of G is bounded by 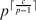$p^{\lceil \frac{c}{p-1} \rceil}$, where c is the nilpotency class of G. Next we give an explicit bound for the order of a finite pk-central p-group of coclass r. Lastly, we establish that for G, a finite p-central p-group, and N, a proper non-maximal normal subgroup of G, the Tate cohomology Hn(G/N, Z(N)) is non-trivial for all n. This final statement answers a question of Schmid concerning groups with non-trivial Tate cohomology.

Keywords

20D15
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 2 , May 2013 , pp. 449 - 456
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013

References

REFERENCES

1.Abdollahi, A., Powerful p-groups have non-inner automorphisms of order p and some cohomology, J. Algebra 323 (2010), 779–789.CrossRefGoogle Scholar
2.Alperin, J. L., A classification of n-abelian groups, Canad. J. Math. 21 (1969), 1238–1244.Google Scholar
3.Camina, R. D., New horizons in pro-p groups, the Nottingham group, Progr. Math. 184 (2000), 205–221.Google Scholar
4.Eick, B., Schur multiplicators of finite p-groups with fixed coclass, Isr. J. Math. 166 (1) (2008), 157–166.CrossRefGoogle Scholar
5.Ellis, G., On the relation between upper central quotients and lower central series of a group, Trans. Am. Math. Soc. 353 (10) (2001), 4219–4234.Google Scholar
6.Fay, T. H. and Walls, G. L., Some remarks on n-potent and n-Abelian groups, J. Indian Math. Soc. (N.S.) 47 (1983), 217–222.Google Scholar
7.Gupta, N. D. and Rhemtulla, A. H., A note on centre-by-finite-exponent varieties of groups, J. Aust. Math. Soc. 11 (1970), 33–36.CrossRefGoogle Scholar
8.Hobby, C., A characteristic subgroup of a p-group, Pacific J. Math. 10 (1960), 853–858.Google Scholar
9.Huppert, B., Endliche Gruppen I (Springer-Verlag, New York, 1967).Google Scholar
10.Isaacs, I. M., Groups with many equal classes, Duke Math. J. 37 (1970), 501–506.Google Scholar
11.Kappe, L.-C., On n-Levi groups, Arch. Math. (Basel) 47 (3) (1986), 198–210.Google Scholar
12.Kappe, L.-C. and Morse, R. F., Levi-properties in Metabelian groups, Contemp. Math. 109 (1990), 59–72.Google Scholar
13.Karpilovsky, G., The Schur multiplier, LMS monographs, new series 2 (Oxford University Press, Oxford, UK, 1987).Google Scholar
14.Mann, A., The exponents of central factors and commutator groups, J. Group Theory 10 (2007), 435–436.Google Scholar
15.Moravec, P., On power endomorphisms of n-central groups, J. Group Theory 9 (2006), 519–536.CrossRefGoogle Scholar
16.Moravec, P., Schur multipliers and power endomorphisms of groups, J. Algebra 308 (2007), 12–25.Google Scholar
17.Moravec, P., On the Schur multipliers of finite p-groups of given coclass, Israel J. Math. 185 (2011), 189–205.Google Scholar
18.Leedham-Green, C. R. and McKay, S., The structure of groups of prime power order, LMS Monographs no. 27 (Oxford University Press, Oxford, UK, 2002).Google Scholar
19.Nickel, W., NQ-nilpotent quotients of finitely presented groups (A refereed GAP 4 package) (1998). http://www.gap-system.org/Packages/nq.htmlGoogle Scholar
20.Schmid, P., A cohomological property of regular p-groups, Mathematische Zeitschrift 175 (1980), 1–3.CrossRefGoogle Scholar
21.Schur, I., Über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen, J. für Math. 127 (1904), 20–50.Google Scholar
22.Thillaisundaram, A., Topics in p-deficiency and p-groups, PhD Thesis (Cambridge University, 2011).Google Scholar
23.Thillaisundaram, A., The automorphism group for p-central p-groups, Int. J. Group Theory 1 (2) (2012), 59–71.Google Scholar
24.Uchida, K., On Tannaka's conjecture on the cohomologically trivial modules, Proc. Japan Acad. 41 (1965), 249–253.Google Scholar
25.Weichsel, P. M., On p-abelian groups, Proc. Am. Math. Soc. 18 (1967), 736–737.Google Scholar