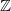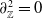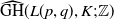1. Introduction
Ozsváth and Szabó’s Heegaard Floer homology [Reference Ozsváth and Szabó20] is undoubtedly one of the most powerful tools of recent discovery in low-dimensional topology. It has far-reaching consequences and has been used to solve long-standing conjectures (for a survey of some results see e.g. [Reference Ozsváth and Szabó21], [Reference Juhász13] and [Reference Hom12]).
Roughly speaking, it associatesFootnote 1 a graded group to a closed and oriented 3-manifold
![]() $Y$
, the Heegaard Floer homology of
$Y$
, the Heegaard Floer homology of
![]() $Y$
, by applying a variant of Lagrangian Floer homology in a high dimensional manifold determined by a Heegaard decomposition of
$Y$
, by applying a variant of Lagrangian Floer homology in a high dimensional manifold determined by a Heegaard decomposition of
![]() $Y$
.
$Y$
.
Soon after its definition, it was realised independently in [Reference Ozsváth and Szabó19] and [Reference Rasmussen24] that a null-homologous knot
![]() $K \subset Y$
induces a filtration on the complex whose homology is the Heegaard Floer homology of
$K \subset Y$
induces a filtration on the complex whose homology is the Heegaard Floer homology of
![]() $Y$
. Furthermore, the filtered quasi-isomorphism type of this complex is an invariant of the couple
$Y$
. Furthermore, the filtered quasi-isomorphism type of this complex is an invariant of the couple
![]() $(Y,K)$
, denoted by
$(Y,K)$
, denoted by
![]() $\mathrm{HFK}(Y,K)$
.
$\mathrm{HFK}(Y,K)$
.
The major computational drawback of these theories lies in the differential, which is defined through a count of pseudo-holomorphic disks with appropriate boundary conditions. Nonetheless, a result of Sarkar and Wang [Reference Sarkar and Wang26] ensures that – after a choice of a suitable doubly pointed Heegaard diagram
![]() $\mathcal{H}$
for
$\mathcal{H}$
for
![]() $(Y,K)$
– the differential can be computed directly from the combinatorics of
$(Y,K)$
– the differential can be computed directly from the combinatorics of
![]() $\mathcal{H}$
. If, moreover,
$\mathcal{H}$
. If, moreover,
![]() $Y$
is a rational homology 3-sphere admitting a Heegaard splitting of genus
$Y$
is a rational homology 3-sphere admitting a Heegaard splitting of genus
![]() $1$
(i.e.
$1$
(i.e.
![]() $Y = S^3$
or
$Y = S^3$
or
![]() $Y$
is a lens space
$Y$
is a lens space
![]() $L(p,q)$
), the homology
$L(p,q)$
), the homology
![]() $\mathrm{HFK}(Y,K)$
admits a neat combinatorial definition, known as grid homology.
$\mathrm{HFK}(Y,K)$
admits a neat combinatorial definition, known as grid homology.
Grid homology in
![]() $S^3$
was pioneered by Manolescu, Oszváth and Sarkar in [Reference Manolescu, Ozsváth and Sarkar14], and for lens spaces by Baker, Hedden and Grigsby in [Reference Baker, Grigsby and Hedden2]; as the name suggests, both the ambient manifold and the knot are encoded in a grid, from which complex and differential for the grid homology can be extracted by simple combinatorial methods.
$S^3$
was pioneered by Manolescu, Oszváth and Sarkar in [Reference Manolescu, Ozsváth and Sarkar14], and for lens spaces by Baker, Hedden and Grigsby in [Reference Baker, Grigsby and Hedden2]; as the name suggests, both the ambient manifold and the knot are encoded in a grid, from which complex and differential for the grid homology can be extracted by simple combinatorial methods.
After establishing the necessary background, in Section 2 we will present the definition of grid homology in lens spaces as given in [Reference Baker, Grigsby and Hedden2]; here, we produce a purely combinatorial proof that
![]() $\partial ^2 = 0$
. Note that the analogous proof in [Reference Baker, Grigsby and Hedden2] is indirect and relies on the well-definedness of the analytic theory.
$\partial ^2 = 0$
. Note that the analogous proof in [Reference Baker, Grigsby and Hedden2] is indirect and relies on the well-definedness of the analytic theory.
The grid homology in lens spaces from [Reference Baker, Grigsby and Hedden2] is only defined over
![]() $\mathbb{F}_2$
. We provide a lift to integer coefficients by proving the existence and uniqueness for sign assignments of grid diagrams. A sign assignment is a coherent choice of sign for each term appearing in the differential of the grid chain complex.
$\mathbb{F}_2$
. We provide a lift to integer coefficients by proving the existence and uniqueness for sign assignments of grid diagrams. A sign assignment is a coherent choice of sign for each term appearing in the differential of the grid chain complex.
Theorem 1.1.
Sign assignments exist on all grids representing a knot
![]() $K\subset L(p,q)$
and can be described combinatorially. Moreover, for a fixed grid diagram, the sign-refined grid homology does not depend on the choice of a sign assignment.
$K\subset L(p,q)$
and can be described combinatorially. Moreover, for a fixed grid diagram, the sign-refined grid homology does not depend on the choice of a sign assignment.
The proof of this theorem is the content of Section 3. The sign refinement of the theory is carried on using a group theoretic reformulation of sign assignments due to Gallais [Reference Gallais10].
Note that the theory developed in this paper is not sufficient to establish the fact that the sign-refined grid homology is an invariant of links in lens spaces (the analogous result in [Reference Baker, Grigsby and Hedden2] follows from an isomorphism with the analytical theory). This flaw has however been addressed more recently in the paper [Reference Tripp28] by Tripp, where invariance of grid homology with integer coefficients is proved.
Finally, in Section 4 we present some computations and examples, together with a description of the programme used to make them. An interactive online version of this programme is freely available on my homepage [Reference Celoria4]. With this tool, we are able to show that small grids (see the discussion in Section 4) have torsion-free grid homologies:
Proposition 1.2. The sign-refined grid homology of knots with small parameters is torsion-free.
This result provides empirical evidence for the absence of torsion in the knot Floer homology of knots in lens spaces. Analogous results for knots in the three sphere have been found by Droz in [Reference Droz9].
2. Grid homology in lens spaces
2.1. Representing knots with grids
In what follows
![]() $p,q$
will always be two coprime integers, and the lens space
$p,q$
will always be two coprime integers, and the lens space
![]() $L(p,q)$
is the (closed, oriented) 3-manifold obtained by
$L(p,q)$
is the (closed, oriented) 3-manifold obtained by
![]() $-\dfrac{p}{q}$
surgery on the unknot
$-\dfrac{p}{q}$
surgery on the unknot
![]() $\bigcirc \subset S^3$
; to avoid confusion, a knot
$\bigcirc \subset S^3$
; to avoid confusion, a knot
![]() $K$
in a 3-manifold
$K$
in a 3-manifold
![]() $Y$
will usually be denoted by
$Y$
will usually be denoted by
![]() $(Y,K)$
.
$(Y,K)$
.

Figure 1. Top-bottom identifications for a 3-dimensional grid for
![]() $L(3,1)$
on the left and
$L(3,1)$
on the left and
![]() $L(3,2)$
on the right.
$L(3,2)$
on the right.
Definition 2.1.
Consider a
![]() $n \times pn$
grid in
$n \times pn$
grid in
![]() $\mathbb{R}^2$
, consisting of the segments
$\mathbb{R}^2$
, consisting of the segments
![]() $\widetilde{\alpha }_i = (tnp, i)$
and
$\widetilde{\alpha }_i = (tnp, i)$
and
![]() $\widetilde{\beta }_j = (j, tn)$
with
$\widetilde{\beta }_j = (j, tn)$
with
![]() $i\in \{ 0, \ldots, n\}, \:j\in \{0, \ldots, np\}$
and
$i\in \{ 0, \ldots, n\}, \:j\in \{0, \ldots, np\}$
and
![]() $t\in [0,1]$
. A twisted grid diagram for
$t\in [0,1]$
. A twisted grid diagram for
![]() $L(p,q)$
is the grid on the torus given by identifying
$L(p,q)$
is the grid on the torus given by identifying
![]() $\widetilde{\beta }_0$
to
$\widetilde{\beta }_0$
to
![]() $\widetilde{\beta }_{pn}$
, and then
$\widetilde{\beta }_{pn}$
, and then
![]() $\widetilde{\alpha }_0$
to
$\widetilde{\alpha }_0$
to
![]() $\widetilde{\alpha }_{n}$
according to a twist depending on
$\widetilde{\alpha }_{n}$
according to a twist depending on
![]() $q$
(see Figure 1
):
$q$
(see Figure 1
):
Here
![]() $s \in [0,pn]$
; the condition
$s \in [0,pn]$
; the condition
![]() $(p,q) = 1$
guarantees that after the identifications the planar grid becomes a toroidal grid.
$(p,q) = 1$
guarantees that after the identifications the planar grid becomes a toroidal grid.
Call
![]() $\alpha = \{ \alpha _i\}$
and
$\alpha = \{ \alpha _i\}$
and
![]() $\beta = \{ \beta _i \}$
with
$\beta = \{ \beta _i \}$
with
![]() $i \in \{1,\ldots,n\}$
the
$i \in \{1,\ldots,n\}$
the
![]() $n$
horizontal (respectively vertical) circles obtained after the identifications in the grid.
$n$
horizontal (respectively vertical) circles obtained after the identifications in the grid.
We can encode a link
![]() $L$
in
$L$
in
![]() $L(p,q)$
by placing a suitable version of the
$L(p,q)$
by placing a suitable version of the
![]() $\mathbb{X}$
’s and
$\mathbb{X}$
’s and
![]() $\mathbb{O}$
’s for grid diagrams in
$\mathbb{O}$
’s for grid diagrams in
![]() $S^3$
: let
$S^3$
: let
![]() $\mathbb{X} = \{ \mathbb{X}_i\}$
and
$\mathbb{X} = \{ \mathbb{X}_i\}$
and
![]() $\mathbb{O} = \{ \mathbb{O}_i\},$
with
$\mathbb{O} = \{ \mathbb{O}_i\},$
with
![]() $i=1, \ldots, n$
be two sets of markings. Put each one of them in the little squaresFootnote 2 of
$i=1, \ldots, n$
be two sets of markings. Put each one of them in the little squaresFootnote 2 of
![]() $G \setminus (\alpha \cup \beta )$
in such a way that each columnFootnote 3 and row contains exactly one element of
$G \setminus (\alpha \cup \beta )$
in such a way that each columnFootnote 3 and row contains exactly one element of
![]() $\,\mathbb{X}$
and one of
$\,\mathbb{X}$
and one of
![]() $\,\mathbb{O}$
, and each square contains at most one marking. By rows and columns here we mean the regions of a grid – homeomorphic to annuli – bounded by two consecutive
$\,\mathbb{O}$
, and each square contains at most one marking. By rows and columns here we mean the regions of a grid – homeomorphic to annuli – bounded by two consecutive
![]() $\alpha$
or
$\alpha$
or
![]() $\beta$
curves, respectively.
$\beta$
curves, respectively.
Now join with a segment each
![]() $\mathbb{X}$
to the
$\mathbb{X}$
to the
![]() $\mathbb{O}$
which lies on the same row, and each
$\mathbb{O}$
which lies on the same row, and each
![]() $\mathbb{O}$
to the
$\mathbb{O}$
to the
![]() $\mathbb{X}$
which lies on the same column (keeping in mind the twisted identification); with this convention, we can encode an orientationFootnote 4 for the link. To get an honest link, just remove self-intersections by converting each self-intersection to an overcrossing of the vertical segments over the horizontal ones (as in Figure 2).
$\mathbb{X}$
which lies on the same column (keeping in mind the twisted identification); with this convention, we can encode an orientationFootnote 4 for the link. To get an honest link, just remove self-intersections by converting each self-intersection to an overcrossing of the vertical segments over the horizontal ones (as in Figure 2).

Figure 2. The link obtained by joining
![]() $\mathbb{X}$
’s and
$\mathbb{X}$
’s and
![]() $\mathbb{O}$
’s in a grid for
$\mathbb{O}$
’s in a grid for
![]() $L(3,2)$
of grid dimension 5. Boxes are delimited by thicker black lines.
$L(3,2)$
of grid dimension 5. Boxes are delimited by thicker black lines.
The grid together with the markings is known as a multipointed Heegaard diagram for
![]() $(L(p,q), K)$
and
$(L(p,q), K)$
and
Remark 2.2. There are two possible ways to connect each
![]() $\mathbb{X}_i$
to the corresponding
$\mathbb{X}_i$
to the corresponding
![]() $\mathbb{O}$
marking on the same row/column, but the isotopy class of the resulting link does not depend upon the possible choices. Indeed, the two links given by these different choices for each row/column are isotopic. This follows at once from the fact that the two possible arcs connecting two markings on the same row/column are – by construction – related by a slide along a meridional disk of the Heegaard decomposition of
$\mathbb{O}$
marking on the same row/column, but the isotopy class of the resulting link does not depend upon the possible choices. Indeed, the two links given by these different choices for each row/column are isotopic. This follows at once from the fact that the two possible arcs connecting two markings on the same row/column are – by construction – related by a slide along a meridional disk of the Heegaard decomposition of
![]() $L(p,q)$
. In other words, the two arcs form a decomposition of the boundary of a disk that defines the given Heegaard splitting.
$L(p,q)$
. In other words, the two arcs form a decomposition of the boundary of a disk that defines the given Heegaard splitting.
The integers
![]() $n,p$
and
$n,p$
and
![]() $q$
will be called the parameters of the grid diagram
$q$
will be called the parameters of the grid diagram
![]() $G$
; the
$G$
; the
![]() $p$
squares of height/length
$p$
squares of height/length
![]() $n$
obtained by cutting the torus along
$n$
obtained by cutting the torus along
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\beta _1$
(in the planar representation of the grid) are called boxes. It is worth to point out that the case in which
$\beta _1$
(in the planar representation of the grid) are called boxes. It is worth to point out that the case in which
![]() $p=1$
and
$p=1$
and
![]() $q=0$
gives as expected a usual grid diagram for a link in
$q=0$
gives as expected a usual grid diagram for a link in
![]() $S^3$
. We will often deliberately forget the distinction between planar and toroidal grids, according to the motto ‘draw on a plane, think on a torus’.
$S^3$
. We will often deliberately forget the distinction between planar and toroidal grids, according to the motto ‘draw on a plane, think on a torus’.
Remark 2.3. Exchanging the role of the markings in a grid representing a knot
![]() $K$
produces a grid diagram for the same link with the opposite orientation on each component.
$K$
produces a grid diagram for the same link with the opposite orientation on each component.
The following result is a consequence of [Reference Baker, Grigsby and Hedden2, Theorem 1.1] and [Reference Cromwell6, Section 2].
Proposition 2.4.
Every link in
![]() $L(p,q)$
can be represented by a grid diagram; two different grid representations of a link differ by a finite number of grid moves analogous to Cromwell moves for grid diagrams in
$L(p,q)$
can be represented by a grid diagram; two different grid representations of a link differ by a finite number of grid moves analogous to Cromwell moves for grid diagrams in
![]() $S^3$
:
$S^3$
:
-
• Translations: these are just vertical and horizontal integer shifts of the grid (respecting the twisted identifications).
-
• (non-interleaving) Commutations: if two adjacent row/columns
 $c_1$
and
$c_1$
and
 $c_2$
are such that the markings of
$c_2$
are such that the markings of
 $c_1$
are contained in a connected component of
$c_1$
are contained in a connected component of
 $c_2$
with the two squares containing the markings removed, then they can be exchanged.
$c_2$
with the two squares containing the markings removed, then they can be exchanged.
-
• (de)Stabilisation: these are the only moves that change the dimension of the grid. There are 8 types of stabilisations, as shown in Figure 3. Destabilisations are just the inverse moves.

Figure 3. Some examples of grid moves; in the top row of the figure, we see four different kinds of stabilisations (there are other four where the roles of the markings are exchanged). In the middle, a schematic example of a row commutation. The bottom part of the figure displays an example of vertical translation in a grid of dimension
![]() $2$
for a knot in
$2$
for a knot in
![]() $L(3,1)$
.
$L(3,1)$
.
The homology class of a knot
![]() $K \subset L(p,q)$
can be read directly from the grid; we just need to keep track of the signed number of intersections of the knot with a meridian of the torus. With the orientation conventions, we have established (so that vertical arcs connect
$K \subset L(p,q)$
can be read directly from the grid; we just need to keep track of the signed number of intersections of the knot with a meridian of the torus. With the orientation conventions, we have established (so that vertical arcs connect
![]() $\mathbb{O}$
’s to
$\mathbb{O}$
’s to
![]() $\mathbb{X}$
’s):
$\mathbb{X}$
’s):
If
![]() $G$
is a grid of parameters
$G$
is a grid of parameters
![]() $(n,p,q)$
, we call
$(n,p,q)$
, we call
![]() $n$
the dimension or grid number of
$n$
the dimension or grid number of
![]() $G$
. The term minimal grid number will be used when referring to the isotopy class of a knot
$G$
. The term minimal grid number will be used when referring to the isotopy class of a knot
![]() $(L(p,q),K)$
; in this case, we mean the quantity
$(L(p,q),K)$
; in this case, we mean the quantity
2.2. Generators of the complex
In the following, we are going to define two different versions (sometimes also known as flavours) of the grid homology for knots in lens spaces. They can both be defined by slight variations in the complex, the ground ring or the differential we will introduce below. For clarity, we are going to restrict ourselves to
![]() $\mathbb{F} = \mathbb{Z}_2$
coefficients until the next section and to knots throughout the paper.
$\mathbb{F} = \mathbb{Z}_2$
coefficients until the next section and to knots throughout the paper.
Definition 2.5.
Given a grid
![]() $G$
of dimension
$G$
of dimension
![]() $n$
representing a knot
$n$
representing a knot
![]() $K \subset L(p,q)$
, the generating set for
$K \subset L(p,q)$
, the generating set for
![]() $G$
is the set
$G$
is the set
![]() $S(G)$
comprising all bijections between
$S(G)$
comprising all bijections between
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
curves. This corresponds to choosing
$\beta$
curves. This corresponds to choosing
![]() $n$
points in
$n$
points in
![]() $\alpha \cap \beta$
such that there is exactly one on each
$\alpha \cap \beta$
such that there is exactly one on each
![]() $\alpha$
and
$\alpha$
and
![]() $ \beta$
curve. There is a bijection
$ \beta$
curve. There is a bijection
which can be described as follows: since we fixed a cyclic labelling of the
![]() $\alpha$
and
$\alpha$
and
![]() $ \beta$
curves, it makes sense to speak of the
$ \beta$
curves, it makes sense to speak of the
![]() $m$
-th intersection between two curves, with
$m$
-th intersection between two curves, with
![]() $0\le m\le p-1$
; so if the
$0\le m\le p-1$
; so if the
![]() $l$
-th component of a generator lies on the
$l$
-th component of a generator lies on the
![]() $m$
-th intersection of
$m$
-th intersection of
![]() $\alpha _l$
and
$\alpha _l$
and
![]() $\beta _j$
, then the permutation
$\beta _j$
, then the permutation
![]() $\sigma \in \mathfrak{S}_n$
associated will be such that
$\sigma \in \mathfrak{S}_n$
associated will be such that
![]() $\sigma (l) = j$
and the
$\sigma (l) = j$
and the
![]() $l$
-th component of
$l$
-th component of
![]() $ \mathbb{Z}_p^n$
will be
$ \mathbb{Z}_p^n$
will be
![]() $m$
(see Figure 4
).
$m$
(see Figure 4
).

Figure 4. Under the bijection described in Definition 2.5, the white generator corresponds to
![]() $((14)(23),(2,1,1,1) )$
, and the black to
$((14)(23),(2,1,1,1) )$
, and the black to
![]() $((34),(0,0,1,2)) \in \mathfrak{S}_4 \times \mathbb{Z}_3^4$
.
$((34),(0,0,1,2)) \in \mathfrak{S}_4 \times \mathbb{Z}_3^4$
.
If
![]() $x \in S(G)$
, we can thus write
$x \in S(G)$
, we can thus write
![]() $x = \left(\sigma _x, \left(x_1^p, \ldots, x_n^p\right)\right)$
; we will refer to
$x = \left(\sigma _x, \left(x_1^p, \ldots, x_n^p\right)\right)$
; we will refer to
![]() $\sigma _x$
as the permutation component of the generator and to
$\sigma _x$
as the permutation component of the generator and to
![]() $\left(x_1^p, \ldots, x_n^p\right)$
as its
$\left(x_1^p, \ldots, x_n^p\right)$
as its
![]() $p$
-coordinates.
$p$
-coordinates.
![]() $S(G)$
can be endowed with a
$S(G)$
can be endowed with a
![]() $ (\mathbb{Q},\mathbb{Q}, \mathbb{Z}_p )$
-valued grading. The first two degrees are known as Maslov and Alexander degrees. The last one is the
$ (\mathbb{Q},\mathbb{Q}, \mathbb{Z}_p )$
-valued grading. The first two degrees are known as Maslov and Alexander degrees. The last one is the
![]() $Spin^c$
degree; since it is preserved by the differential (Proposition 2.11), it will provide a splitting of the complex into
$Spin^c$
degree; since it is preserved by the differential (Proposition 2.11), it will provide a splitting of the complex into
![]() $p$
direct summands. All these degrees are going to be defined in a purely combinatorial way.
$p$
direct summands. All these degrees are going to be defined in a purely combinatorial way.
Definition 2.6.
Let
![]() $A$
and
$A$
and
![]() $B$
denote two finite sets of points in
$B$
denote two finite sets of points in
![]() $\mathbb{R}^2$
; let
$\mathbb{R}^2$
; let
![]() $\mathcal{I}(A, B)$
be the number of pairs
$\mathcal{I}(A, B)$
be the number of pairs
such that
![]() $a_i\lt b_i$
for
$a_i\lt b_i$
for
![]() $i=1,2$
.
$i=1,2$
.
Denote by
![]() $X(p,n)$
(respectively
$X(p,n)$
(respectively
![]() $Y(p,n)$
) the set of
$Y(p,n)$
) the set of
![]() $n$
-tuples (respectively
$n$
-tuples (respectively
![]() $pn$
-tuples) of points contained in the
$pn$
-tuples) of points contained in the
![]() $n \times pn$
(respectively
$n \times pn$
(respectively
![]() $pn \times pn$
) rectangle in
$pn \times pn$
) rectangle in
![]() $\mathbb{R}^2$
whose bottom vertices are
$\mathbb{R}^2$
whose bottom vertices are
![]() $(0,0)$
and
$(0,0)$
and
![]() $(pn,0 )$
; then define
$(pn,0 )$
; then define
as the function sending a
![]() $n$
-tuple
$n$
-tuple
![]() $\{ (c_i, b_i) \}_{i=1, \ldots, n}$
to the
$\{ (c_i, b_i) \}_{i=1, \ldots, n}$
to the
![]() $pn$
-tuple
$pn$
-tuple
In order to avoid notational overloads, we are going to write
![]() $\widetilde{x}$
instead of
$\widetilde{x}$
instead of
![]() $C_{p,q}(x)$
; one example of such a function is described in Figure 5.
$C_{p,q}(x)$
; one example of such a function is described in Figure 5.

Figure 5. A representation of the action of
![]() $C_{p,q}$
for
$C_{p,q}$
for
![]() $(p,q) =(3,1)$
and
$(p,q) =(3,1)$
and
![]() $(3,2)$
(on the left and right, respectively).
$(3,2)$
(on the left and right, respectively).
We can then define the Maslov degree as follows:
In the equation above,
![]() $d(p,q,q-1)$
is a rational number known as the correction term of
$d(p,q,q-1)$
is a rational number known as the correction term of
![]() $L(p,q)$
associated with the
$L(p,q)$
associated with the
![]() $(q-1)$
-th
$(q-1)$
-th
![]() $Spin^c$
structure; as explained in [Reference Ozsváth and Szabó18, Prop. 4.8], it can be computed recursively as follows:Footnote 5
$Spin^c$
structure; as explained in [Reference Ozsváth and Szabó18, Prop. 4.8], it can be computed recursively as follows:Footnote 5
-
•
 $d(1,0,0) = 0$
$d(1,0,0) = 0$
-
•
 $d(p,q,i) = \left ( \frac{pq - (2i +1 -p - q)^2}{4pq} \right ) + d(q,r,j)$
where
$d(p,q,i) = \left ( \frac{pq - (2i +1 -p - q)^2}{4pq} \right ) + d(q,r,j)$
where
 $r$
and
$r$
and
 $j$
denote the reduction of
$j$
denote the reduction of
 $p$
and
$p$
and
 $i$
$i$
 $(\text{mod } \,q)$
.
$(\text{mod } \,q)$
.
Similarly, the Alexander grading can be defined as:
By slightly modifying the differential we will introduce in the next section,
![]() $A$
can be demoted to a filtration on the complex, rather than a degree. The complexes we are going to consider should be thought of as the graded objects associated with this filtration.
$A$
can be demoted to a filtration on the complex, rather than a degree. The complexes we are going to consider should be thought of as the graded objects associated with this filtration.
Remark 2.7. Note that equation (2) is not the standard formula used to define
![]() $A$
; here we are using the fact (see [Reference Degany, Freimuth and Trefts8, Sec. 2]) that in a grid of dimension
$A$
; here we are using the fact (see [Reference Degany, Freimuth and Trefts8, Sec. 2]) that in a grid of dimension
![]() $n$
for a knot in
$n$
for a knot in
![]() $S^3$
$S^3$
with
![]() $J = \mathbb{O}$
or
$J = \mathbb{O}$
or
![]() $\mathbb{X}$
, and
$\mathbb{X}$
, and
![]() $x$
is any generator in
$x$
is any generator in
![]() $S(G)$
.
$S(G)$
.
Now call
![]() $\left(a_1^{\mathbb{O}}, \ldots, a_n^{\mathbb{O}}\right)$
the
$\left(a_1^{\mathbb{O}}, \ldots, a_n^{\mathbb{O}}\right)$
the
![]() $p$
-coordinates of the generator whose components are in the lower left vertex of the squares which contain a
$p$
-coordinates of the generator whose components are in the lower left vertex of the squares which contain a
![]() $\mathbb{O}$
marking. The
$\mathbb{O}$
marking. The
![]() $Spin^c$
degree of
$Spin^c$
degree of
![]() $x = (\sigma _x, (a_1, \ldots, a_n) ) \in S(G)$
is defined as:
$x = (\sigma _x, (a_1, \ldots, a_n) ) \in S(G)$
is defined as:
We are implicitly using a canonical identification between
![]() $Spin^c (L(p,q))$
and
$Spin^c (L(p,q))$
and
![]() $\mathbb{Z}_p$
(cf. [Reference Ozsváth and Szabó18, Sec. 4.1]).
$\mathbb{Z}_p$
(cf. [Reference Ozsváth and Szabó18, Sec. 4.1]).
It is clear from the definition that the Alexander grading depends on the placement of all the markings, while
![]() $M$
and
$M$
and
![]() $S$
only on the position of the
$S$
only on the position of the
![]() $\mathbb{O}$
s.
$\mathbb{O}$
s.
Let
![]() $R = \mathbb{F} [V_1, \ldots, V_n]$
denote the ring of
$R = \mathbb{F} [V_1, \ldots, V_n]$
denote the ring of
![]() $n$
-variable polynomials with
$n$
-variable polynomials with
![]() $\mathbb{F}$
coefficients, and
$\mathbb{F}$
coefficients, and
![]() $\widehat{R} ={R}/{\{ V_1 = 0\}}$
. These
$\widehat{R} ={R}/{\{ V_1 = 0\}}$
. These
![]() $V$
variablesFootnote 6 are graded endomorphisms of the complex; their function is to ‘keep track’ of the
$V$
variablesFootnote 6 are graded endomorphisms of the complex; their function is to ‘keep track’ of the
![]() $\mathbb{O}$
markings in the differential.
$\mathbb{O}$
markings in the differential.
We can now define at least the underlying module structure of the complexes we are going to use in what follows:
Definition 2.8.
The minus complex
![]() $\mathrm{GC}^-(G)$
is the free
$\mathrm{GC}^-(G)$
is the free
![]() $R$
-module generated over
$R$
-module generated over
![]() $S(G)$
. The hat complex
$S(G)$
. The hat complex
![]() $\widehat{\mathrm{GC}}(G)$
is the free
$\widehat{\mathrm{GC}}(G)$
is the free
![]() $\widehat{R}$
-module generated over
$\widehat{R}$
-module generated over
![]() $S(G)$
. Extend the gradings to the whole module by setting the behaviour of the action for the variables in the ground ring:
$S(G)$
. Extend the gradings to the whole module by setting the behaviour of the action for the variables in the ground ring:
-
 $A(Vx) = A(x) - 1$
$A(Vx) = A(x) - 1$
-
 $M(V x) = M(x) - 2$
$M(V x) = M(x) - 2$
-
 $S(V x) = S(x)$
$S(V x) = S(x)$
where
![]() $V$
is any of the
$V$
is any of the
![]() $V_i$
.
$V_i$
.
Example 2.9. In this example, we are going to exhibit the generating set of the grid
![]() $G$
on the left of Figure 6, in the 0-th
$G$
on the left of Figure 6, in the 0-th
![]() $Spin^c$
structure, which we are going to denote by
$Spin^c$
structure, which we are going to denote by
![]() $S(G,0)$
.
$S(G,0)$
.
![]() $S(G,0)$
consists of four elements (see also Figure 7):
$S(G,0)$
consists of four elements (see also Figure 7):
The notation
![]() $\mathbb{F}_{[a,b]}$
denotes a generator having
$\mathbb{F}_{[a,b]}$
denotes a generator having
![]() $(M,A) = (a,b)$
bi-degree.
$(M,A) = (a,b)$
bi-degree.

Figure 7. The generating set
![]() $S(G,0)$
, with the bi-degree
$S(G,0)$
, with the bi-degree
![]() $(M,A)$
, on the axes is displayed on the left. On the right instead, we have the underlying modules for the complexes
$(M,A)$
, on the axes is displayed on the left. On the right instead, we have the underlying modules for the complexes
![]() $\widehat{\mathrm{GC}} (G,0) = \mathrm{GC}^- (G,0)$
with axes labelled by powers of the
$\widehat{\mathrm{GC}} (G,0) = \mathrm{GC}^- (G,0)$
with axes labelled by powers of the
![]() $V$
variables and Alexander degree. The dots represent generators over
$V$
variables and Alexander degree. The dots represent generators over
![]() $\mathbb{F}$
.
$\mathbb{F}$
.
2.3. The differential
As already mentioned in the introduction, grid homology hinges upon Sarkar and Wang’s main result in [Reference Sarkar and Wang26]; in their terminology, (twisted) grid diagrams are nice (multipointed, genus 1) Heegaard diagram for
![]() $L(p,q)$
, so the differential of
$L(p,q)$
, so the differential of
![]() $\mathrm{CFK}$
can be computed combinatorially. In this setting, the holomorphic disks of knot Floer homology’s differential take the milder form of embedded rectangles on the grid.
$\mathrm{CFK}$
can be computed combinatorially. In this setting, the holomorphic disks of knot Floer homology’s differential take the milder form of embedded rectangles on the grid.
Consider two generators
![]() $x,y \in S(G)$
having the same
$x,y \in S(G)$
having the same
![]() $Spin^c$
degree; if the permutations associated with
$Spin^c$
degree; if the permutations associated with
![]() $x$
and
$x$
and
![]() $y$
differ by a transposition, then the two components where the generators differ are the vertices of four immersed rectangles
$y$
differ by a transposition, then the two components where the generators differ are the vertices of four immersed rectangles
![]() $r_1, \ldots,r_4$
in the grid; the sides of the
$r_1, \ldots,r_4$
in the grid; the sides of the
![]() $r_i$
’s are alternately arcs on the
$r_i$
’s are alternately arcs on the
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
curves. We can fix a direction for such a rectangle
$\beta$
curves. We can fix a direction for such a rectangle
![]() $r$
, by prescribing that
$r$
, by prescribing that
![]() $r$
goes from
$r$
goes from
![]() $x$
to
$x$
to
![]() $y$
if its lower left and upper-right corners are on
$y$
if its lower left and upper-right corners are on
![]() $x$
components. Therefore, if
$x$
components. Therefore, if
![]() $x$
and
$x$
and
![]() $y$
are two generators in the same
$y$
are two generators in the same
![]() $Spin^c$
degree, and differing by a single transposition, there are exactly two directed rectangles from
$Spin^c$
degree, and differing by a single transposition, there are exactly two directed rectangles from
![]() $x$
to
$x$
to
![]() $y$
.
$y$
.
Definition 2.10.
Given a grid
![]() $G$
, and
$G$
, and
![]() $x,y \in S(G)$
, call
$x,y \in S(G)$
, call
![]() $Rect(x,y)$
the set of directed rectangles connecting
$Rect(x,y)$
the set of directed rectangles connecting
![]() $x$
to
$x$
to
![]() $y$
; we will denote by
$y$
; we will denote by
the set of all directed rectangles between generators in
![]() $G$
. Similarly,
$G$
. Similarly,
![]() $Rect^\circ (G)$
is going to be the set of empty rectangles, that is those
$Rect^\circ (G)$
is going to be the set of empty rectangles, that is those
![]() $ r \in Rect(x,y)$
such that
$ r \in Rect(x,y)$
such that
![]() $ Int(r) \cap x = \emptyset$
.
$ Int(r) \cap x = \emptyset$
.
Note that by assumption if
![]() $r \in Rect^\circ (x,y)$
, then it does not contain any point of
$r \in Rect^\circ (x,y)$
, then it does not contain any point of
![]() $y$
either, so in particular it is embedded in the torus composed by the grid.
$y$
either, so in particular it is embedded in the torus composed by the grid.
One example of two rectangles is displayed in Figure 8. If
![]() $x,y \in S(G)$
, then
$x,y \in S(G)$
, then
![]() $|Rect(x,y)|\in \{0,2\}$
, and we will prove in Proposition 2.11 that it can be non-zero only for generators in the same
$|Rect(x,y)|\in \{0,2\}$
, and we will prove in Proposition 2.11 that it can be non-zero only for generators in the same
![]() $Spin^c$
degree which differ by a single transposition. On the other hand, with the same hypothesis on the generators,
$Spin^c$
degree which differ by a single transposition. On the other hand, with the same hypothesis on the generators,
![]() $|Rect^\circ (x,y)| \in \{0,1,2\}$
.
$|Rect^\circ (x,y)| \in \{0,1,2\}$
.

Figure 8. Two directed rectangles connecting
![]() $x$
(white) to
$x$
(white) to
![]() $y$
(black) in a grid of parameters (4, 3, 1). Only the horizontal one (in blue) is empty.
$y$
(black) in a grid of parameters (4, 3, 1). Only the horizontal one (in blue) is empty.
If
![]() $r_1 \in Rect(x,y)$
and
$r_1 \in Rect(x,y)$
and
![]() $r_2 \in Rect(y,z)$
, we can consider their concatenation
$r_2 \in Rect(y,z)$
, we can consider their concatenation
![]() $r_1 \ast r_2$
, which we call a polygon connecting
$r_1 \ast r_2$
, which we call a polygon connecting
![]() $x$
to
$x$
to
![]() $z$
through
$z$
through
![]() $y$
. We are going to denote by
$y$
. We are going to denote by
![]() $Poly(x,z)$
the set of polygons connecting
$Poly(x,z)$
the set of polygons connecting
![]() $x$
to
$x$
to
![]() $z$
, and by
$z$
, and by
![]() $Poly^\circ (x,z)$
the empty ones. If
$Poly^\circ (x,z)$
the empty ones. If
![]() $P$
is an empty rectangle or polygon, denote by
$P$
is an empty rectangle or polygon, denote by
![]() $O_i(P)$
the number of times (with multiplicity) that the
$O_i(P)$
the number of times (with multiplicity) that the
![]() $i$
-th
$i$
-th
![]() $\mathbb{O}$
marking appears in
$\mathbb{O}$
marking appears in
![]() $P$
. Note that for a grid diagram of a knot in either
$P$
. Note that for a grid diagram of a knot in either
![]() $S^3$
or a lens space, we have
$S^3$
or a lens space, we have
![]() $O_i(P)\in \{0,1,2\}$
.
$O_i(P)\in \{0,1,2\}$
.
The differential on
![]() $\mathrm{GC}^-(G)$
and
$\mathrm{GC}^-(G)$
and
![]() $\widehat{\mathrm{GC}}(G)$
is just going to be a count of empty rectangles, satisfying some additional constraints according to the flavour chosen. For the two flavours of grid homology considered here (keep in mind that for
$\widehat{\mathrm{GC}}(G)$
is just going to be a count of empty rectangles, satisfying some additional constraints according to the flavour chosen. For the two flavours of grid homology considered here (keep in mind that for
![]() $\widehat{\mathrm{GC}}$
we set
$\widehat{\mathrm{GC}}$
we set
![]() $V_1 = 0$
), we keep track of the
$V_1 = 0$
), we keep track of the
![]() $\mathbb{O}$
markings contained in the rectangles, by multiplying with the corresponding variable
$\mathbb{O}$
markings contained in the rectangles, by multiplying with the corresponding variable
![]() $V_i$
:
$V_i$
:
 \begin{equation}\partial (x) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x,y) \\ r \cap \mathbb{X} = \emptyset} } \left(\prod_{i=1}^n V_i^{O_i(r)} \right) y\end{equation}
\begin{equation}\partial (x) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x,y) \\ r \cap \mathbb{X} = \emptyset} } \left(\prod_{i=1}^n V_i^{O_i(r)} \right) y\end{equation}
Proposition 2.11.
Given a grid diagram
![]() $G$
of parameters
$G$
of parameters
![]() $(n,p,q)$
, the modules
$(n,p,q)$
, the modules
![]() $\mathrm{GC}^- (G)$
and
$\mathrm{GC}^- (G)$
and
![]() $\widehat{\mathrm{GC}} (G)$
endowed with the endomorphism
$\widehat{\mathrm{GC}} (G)$
endowed with the endomorphism
![]() $\partial$
are chain complexes, that is
$\partial$
are chain complexes, that is
![]() $\partial ^2 = 0$
in both cases. Moreover,
$\partial ^2 = 0$
in both cases. Moreover,
![]() $\partial$
acts on the tri-grading as follows:
$\partial$
acts on the tri-grading as follows:
-
1.
 $S(\partial (x)) = S(x)$
$S(\partial (x)) = S(x)$
-
2.
 $M(\partial (x)) = M(x) -1$
$M(\partial (x)) = M(x) -1$
-
3.
 $A(\partial (x)) = A(x)$
$A(\partial (x)) = A(x)$
Remark 2.12. This Proposition is implicit in [Reference Baker, Grigsby and Hedden2], and it can be seen as a direct consequence of Theorem 1.1 therein; however, some of the considerations in this proof will be useful in the following section. Moreover, this proof will rely only on combinatorics, showing that the result can be obtained without any reference to the holomorphic theory of [Reference Ozsváth and Szabó19] and [Reference Rasmussen24].
Proof. We begin by examining the behaviour of the degrees under the differential; condition (1) is easy to prove: by equation (3), the only relevant part of a generator
![]() $x$
for the computation of
$x$
for the computation of
![]() $S(x)$
is given by its
$S(x)$
is given by its
![]() $p$
-coordinates. If
$p$
-coordinates. If
![]() $y$
appears in the differential of
$y$
appears in the differential of
![]() $x$
, call
$x$
, call
![]() $a_i^x,a_i^y, a_j^x$
and
$a_i^x,a_i^y, a_j^x$
and
![]() $a_j^y$
the
$a_j^y$
the
![]() $p$
-coordinates where
$p$
-coordinates where
![]() $x$
and
$x$
and
![]() $y$
differ. If
$y$
differ. If
![]() $a_i^x = k$
and
$a_i^x = k$
and
![]() $a_j^x = l$
, with
$a_j^x = l$
, with
![]() $k,l \in \mathbb{Z}_p$
, then (since by hypothesis they are connected by a rectangle)
$k,l \in \mathbb{Z}_p$
, then (since by hypothesis they are connected by a rectangle)
![]() $a_i^y = k + t$
and
$a_i^y = k + t$
and
![]() $a_j^y = l-t$
modulo
$a_j^y = l-t$
modulo
![]() $p$
for some
$p$
for some
![]() $t \in \{0,\ldots, p-1\}$
(as shown in Figure 9); so
$t \in \{0,\ldots, p-1\}$
(as shown in Figure 9); so
![]() $S(x)=S(y)$
.
$S(x)=S(y)$
.

Figure 9. The non-equal
![]() $p$
-coordinates of the generators compensate each other.
$p$
-coordinates of the generators compensate each other.
Let’s now see what happens for the other two degrees; if
![]() $x$
and
$x$
and
![]() $y$
are generators in
$y$
are generators in
![]() $G$
connected by an empty rectangle
$G$
connected by an empty rectangle
![]() $r$
, directed from
$r$
, directed from
![]() $x$
to
$x$
to
![]() $y$
, then their lifts
$y$
, then their lifts
![]() $\widetilde{x}$
and
$\widetilde{x}$
and
![]() $\widetilde{y}$
will differ in
$\widetilde{y}$
will differ in
![]() $2p$
positions, according to the pattern suggested in Figure 10.
$2p$
positions, according to the pattern suggested in Figure 10.

Figure 10. The difference between the functions
![]() $\mathcal{I}(x,*)$
and
$\mathcal{I}(x,*)$
and
![]() $\mathcal{I}(y,*)$
for two generators (in black and white respectively) whose permutations differ by a transposition. The shading indicates the upper-right regions considered in the computation of the function
$\mathcal{I}(y,*)$
for two generators (in black and white respectively) whose permutations differ by a transposition. The shading indicates the upper-right regions considered in the computation of the function
![]() $\mathcal{I}$
.
$\mathcal{I}$
.
This implies that the corresponding
![]() $\mathcal{I}$
function will change accordingly:
$\mathcal{I}$
function will change accordingly:
Moreover, the same result holds with
![]() $\mathbb{X}$
markings instead of
$\mathbb{X}$
markings instead of
![]() $\mathbb{O}$
’s. Then from equation (4), we get for (2) and (3), respectively:
$\mathbb{O}$
’s. Then from equation (4), we get for (2) and (3), respectively:
 \begin{equation*}\displaystyle M(\partial (x)) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x,y) \\ r \cap \mathbb{X} = \emptyset}} \left( \sum_{i=1}^n -2 O_i (r) \right) M(y)\end{equation*}
\begin{equation*}\displaystyle M(\partial (x)) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x,y) \\ r \cap \mathbb{X} = \emptyset}} \left( \sum_{i=1}^n -2 O_i (r) \right) M(y)\end{equation*}
 \begin{equation*}\displaystyle A(\partial (x)) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x,y) \\ r \cap \mathbb{X} = \emptyset}} \left(\sum_{i=1}^n - O_i (r)\right) A(y)\end{equation*}
\begin{equation*}\displaystyle A(\partial (x)) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x,y) \\ r \cap \mathbb{X} = \emptyset}} \left(\sum_{i=1}^n - O_i (r)\right) A(y)\end{equation*}
A substitution using equations (1) and (2) defining the Maslov and Alexander degrees yields (2) and (3).
We are left to show that
![]() $ \partial ^2 =0$
; we thus need to study the possible decompositions in rectangles of polygons connecting two generators.
$ \partial ^2 =0$
; we thus need to study the possible decompositions in rectangles of polygons connecting two generators.
We will prove the result for the minus flavoured complex, since the analogous result for the hat version follows immediately. From equation (4), we can compute
 \begin{equation}\partial^2 (x) = \sum_{z \in S(G)} \sum_{\substack{\psi \in Poly^\circ (x, z) \\ \psi \cap \mathbb{X} = \emptyset}} N(\psi) \left( \prod_{i=1}^{n} {V_i}^{O_i (\psi)} \right) z\end{equation}
\begin{equation}\partial^2 (x) = \sum_{z \in S(G)} \sum_{\substack{\psi \in Poly^\circ (x, z) \\ \psi \cap \mathbb{X} = \emptyset}} N(\psi) \left( \prod_{i=1}^{n} {V_i}^{O_i (\psi)} \right) z\end{equation}
where
![]() $\psi$
is a polygon connecting
$\psi$
is a polygon connecting
![]() $x$
to
$x$
to
![]() $z$
, and
$z$
, and
![]() $N(\psi )$
is the number of possible ways of writing
$N(\psi )$
is the number of possible ways of writing
![]() $\psi$
as the composition of two empty rectangles
$\psi$
as the composition of two empty rectangles
![]() $r_1 \ast r_2$
, with
$r_1 \ast r_2$
, with
![]() $r_1 \in Rect^\circ (x,y)$
and
$r_1 \in Rect^\circ (x,y)$
and
![]() $r_2 \in Rect^\circ (y,z)$
for some
$r_2 \in Rect^\circ (y,z)$
for some
![]() $y\in S(G)$
.
$y\in S(G)$
.
Note that a polygon
![]() $P$
connecting two generators is empty if and only if both the rectangles
$P$
connecting two generators is empty if and only if both the rectangles
![]() $P$
is made of are empty as well. In order to complete the proof, we need to show that
$P$
is made of are empty as well. In order to complete the proof, we need to show that
![]() $ N(\psi ) \equiv 0 \;(\mbox{mod}\;2)$
, that is, there is an even number of ways (in fact exactly
$ N(\psi ) \equiv 0 \;(\mbox{mod}\;2)$
, that is, there is an even number of ways (in fact exactly
![]() $2$
) to decompose into rectangles a fixed
$2$
) to decompose into rectangles a fixed
![]() $\psi$
that appears in the squared differential
$\psi$
that appears in the squared differential
![]() $\partial ^2$
. We can also take advantage of the proof in [Reference Ozsváth, Stipsicz and Szabó22, Lemma
$\partial ^2$
. We can also take advantage of the proof in [Reference Ozsváth, Stipsicz and Szabó22, Lemma
![]() $4.4.6$
] to reduce the number of cases to examine; as a matter of fact, if a polygon
$4.4.6$
] to reduce the number of cases to examine; as a matter of fact, if a polygon
![]() $\psi$
does not cross one of the
$\psi$
does not cross one of the
![]() $\alpha$
curves, we can cut the torus open along it, and think of the polygon as living in a portion of an
$\alpha$
curves, we can cut the torus open along it, and think of the polygon as living in a portion of an
![]() $np\times np$
grid for
$np\times np$
grid for
![]() $S^3$
. Thus, we only need to worry about polygons that intersect all
$S^3$
. Thus, we only need to worry about polygons that intersect all
![]() $\alpha$
circles.
$\alpha$
circles.
There are then four possibilities to be considered a priori, according to the quantity
![]() $M= |x\setminus (x \cap z)| \in \{ 0, \ldots, 4\}$
, as schematically shown in Figure 11.
$M= |x\setminus (x \cap z)| \in \{ 0, \ldots, 4\}$
, as schematically shown in Figure 11.

Figure 11. A representation of the possibilities for
![]() $M$
(in a grid of dimension
$M$
(in a grid of dimension
![]() $4$
). The circles correspond (from larger to smaller) to the components of generators
$4$
). The circles correspond (from larger to smaller) to the components of generators
![]() $x,y$
and
$x,y$
and
![]() $z$
. Two circles are concentric whenever the corresponding components of the generators coincide, and the
$z$
. Two circles are concentric whenever the corresponding components of the generators coincide, and the
![]() $i$
-th row shows the relative position for the components of the generators lying on
$i$
-th row shows the relative position for the components of the generators lying on
![]() $\alpha _i$
.
$\alpha _i$
.
If
![]() $M = 0$
, that is
$M = 0$
, that is
![]() $x = z$
, the only possible polygons are thin rectangles, called
$x = z$
, the only possible polygons are thin rectangles, called
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
degenerations or simply
$\beta$
degenerations or simply
![]() $\alpha/\beta$
-strips (see e.g. Figure 17). These are strips of respectively height or width
$\alpha/\beta$
-strips (see e.g. Figure 17). These are strips of respectively height or width
![]() $1$
(otherwise they would not be empty). We are not concerned with these strips, since each of them contains exactly one
$1$
(otherwise they would not be empty). We are not concerned with these strips, since each of them contains exactly one
![]() $\mathbb{X}$
marking; hence, they do not contribute to the differential.
$\mathbb{X}$
marking; hence, they do not contribute to the differential.
This is not true for the filtered versions of these complexes (see [Reference Ozsváth, Stipsicz and Szabó22, Ch. 13]). Nonetheless, the polygons that cannot be split in two different ways cancel each other out nicely in that case as well. As an aside, we note here that there is only one way to decompose such a strip into two rectangles (one starting from
![]() $x$
, and one arriving to it).
$x$
, and one arriving to it).
The case
![]() $M = 1$
can be dismissed too, since rectangles only connect generators which differ in exactly two points.Footnote 7
$M = 1$
can be dismissed too, since rectangles only connect generators which differ in exactly two points.Footnote 7
If
![]() $M = 4$
, that is, the corners of the two rectangles are all distinct, we can apply the same approach of [Reference Ozsváth, Stipsicz and Szabó22, Ch. 4]; there are two ways of counting them, as shown in Figure 12.
$M = 4$
, that is, the corners of the two rectangles are all distinct, we can apply the same approach of [Reference Ozsváth, Stipsicz and Szabó22, Ch. 4]; there are two ways of counting them, as shown in Figure 12.

Figure 12. When
![]() $M=4$
, we can consider the two rectangles (from white to black) in either order, by choosing a suitable intermediate generator
$M=4$
, we can consider the two rectangles (from white to black) in either order, by choosing a suitable intermediate generator
![]() $y$
(gray).
$y$
(gray).
Basically, the two decompositions correspond to taking the two rectangles in either order. We remark that one rectangle might wrap around the other, but the number of decompositions does not depend on this wrapping.
The case
![]() $M=2$
needs a bit more care, since it has no
$M=2$
needs a bit more care, since it has no
![]() $S^3$
counterpart (see [Reference Ozsváth, Stipsicz and Szabó22, Ch. 4]). In this case, the two rectangles must share part of 2 edges. There are two possibilities to consider:
$S^3$
counterpart (see [Reference Ozsváth, Stipsicz and Szabó22, Ch. 4]). In this case, the two rectangles must share part of 2 edges. There are two possibilities to consider:
-
1. the rectangle starting from
 $x$
does not cross all
$x$
does not cross all
 $\alpha$
curves. Up to vertical/horizontal translations, it can be placed in such a way that it does not intersect the boundary of the planar grid.
$\alpha$
curves. Up to vertical/horizontal translations, it can be placed in such a way that it does not intersect the boundary of the planar grid. -
2. the rectangle starting from
 $x$
intersects all the
$x$
intersects all the
 $\alpha$
curves at least once.
$\alpha$
curves at least once.
Either way, the second rectangle joining the intermediate generator to
![]() $z$
must end and start on the same
$z$
must end and start on the same
![]() $\alpha$
curves of the first rectangle; the configurations in both cases are shown in Figure 13, together with their decompositions.
$\alpha$
curves of the first rectangle; the configurations in both cases are shown in Figure 13, together with their decompositions.

Figure 13. Relevant combinatorial possibilities for
![]() $M=2$
on a grid for
$M=2$
on a grid for
![]() $L(3,1)$
. On each row, the two possible decompositions are shown. Again we adopt the convention
$L(3,1)$
. On each row, the two possible decompositions are shown. Again we adopt the convention
![]() $x,y,z$
= white, grey and black dots, showing only the appropriate components.
$x,y,z$
= white, grey and black dots, showing only the appropriate components.
Lastly, if
![]() $M=3$
we can again distinguish two possibilities as in the previous case; the combinatorially inequivalent configurations are shown in Figure 14, together with their two decompositions.
$M=3$
we can again distinguish two possibilities as in the previous case; the combinatorially inequivalent configurations are shown in Figure 14, together with their two decompositions.

Figure 14. Some configurations for the
![]() $M=3$
case. The complete combinatorial classification up to wrapping is presented in Figure 20.
$M=3$
case. The complete combinatorial classification up to wrapping is presented in Figure 20.
Example 2.13. We continue here the computations of the grid from Example 2.9: we can now complete the picture by adding the differentials and computing the various homologies. We have (cf. Figure 15):
-
 $\partial (a) = \partial (b) = 0$
$\partial (a) = \partial (b) = 0$
-
 $\partial (c) = a+b$
$\partial (c) = a+b$
-
 $\partial (d) = V_1a + V_2 b$
$\partial (d) = V_1a + V_2 b$
It is then an easy task to compute the grid homologies in the two flavours:
2.4. The homologies
From the definitions given up to now, it might seem strange that the homology of such a complex could be an invariant of the smooth isotopy type of a knot, since even the ground ring depends on the dimension of a grid representing it; Theorem 2.15 below ensures however that
![]() $\mathrm{GH}^-$
and
$\mathrm{GH}^-$
and
![]() $\widehat{\mathrm{GH}}$
are quasi-isomorphic to a finitely generated
$\widehat{\mathrm{GH}}$
are quasi-isomorphic to a finitely generated
![]() $\mathbb{F} [U]$
and
$\mathbb{F} [U]$
and
![]() $\mathbb{F}$
-modules, respectively (see e.g. Figure 15). The algebraic reason behind this is the content of the following Proposition:
$\mathbb{F}$
-modules, respectively (see e.g. Figure 15). The algebraic reason behind this is the content of the following Proposition:
Proposition 2.14.
Let
![]() $G$
be a grid of parameters
$G$
be a grid of parameters
![]() $(n, p,q)$
for a knot
$(n, p,q)$
for a knot
![]() $K$
. Then, the action of multiplication by
$K$
. Then, the action of multiplication by
![]() $V_i$
on the complex
$V_i$
on the complex
![]() $\mathrm{GC}^- (G)$
is quasi-isomorphic to multiplication by
$\mathrm{GC}^- (G)$
is quasi-isomorphic to multiplication by
![]() $V_j$
.
$V_j$
.
Proof. See [Reference Ozsváth, Stipsicz and Szabó22, Ch. 4].
Theorem 2.15. (Thm. 1.1 in [Reference Baker, Grigsby and Hedden2]) The homologies
and
regarded as
![]() $(\mathbb{Q},\mathbb{Q},\mathbb{Z}_p)$
graded modules over the appropriate ring are invariants of the knot
$(\mathbb{Q},\mathbb{Q},\mathbb{Z}_p)$
graded modules over the appropriate ring are invariants of the knot
![]() $(L(p,q), K)$
. Moreover,
$(L(p,q), K)$
. Moreover,
![]() $ (\mathrm{GC}^- (G), \partial )$
is quasi-isomorphic to a finitely generated
$ (\mathrm{GC}^- (G), \partial )$
is quasi-isomorphic to a finitely generated
![]() $\mathbb{F} [U]$
module, where
$\mathbb{F} [U]$
module, where
![]() $U$
acts as any of the
$U$
acts as any of the
![]() $V_i$
, and
$V_i$
, and
![]() $(\widehat{\mathrm{GC}}, \partial )$
is quasi-isomorphic to a finitely generated
$(\widehat{\mathrm{GC}}, \partial )$
is quasi-isomorphic to a finitely generated
![]() $\mathbb{F}$
module.
$\mathbb{F}$
module.

Figure 15. On the left the complex
![]() $\widehat{\mathrm{GC}} (G,0)$
and on the right the complex
$\widehat{\mathrm{GC}} (G,0)$
and on the right the complex
![]() $\mathrm{GC}^- (G,0)$
, for the grid
$\mathrm{GC}^- (G,0)$
, for the grid
![]() $G$
from Example 2.9, the dotted line corresponds to multiplication by
$G$
from Example 2.9, the dotted line corresponds to multiplication by
![]() $V_2$
, and the dashed one to multiplication by
$V_2$
, and the dashed one to multiplication by
![]() $V_1$
. Non-trivial elements in homology are circled in red.
$V_1$
. Non-trivial elements in homology are circled in red.
Due to this theorem, we will sometimes make the notational abuse of writing
![]() $\widehat{\mathrm{GH}} (L(p,q), K)$
instead of
$\widehat{\mathrm{GH}} (L(p,q), K)$
instead of
![]() $\widehat{\mathrm{GH}} (G)$
,
$\widehat{\mathrm{GH}} (G)$
,
![]() $G$
being a grid of parameters
$G$
being a grid of parameters
![]() $(n,p,q)$
representing
$(n,p,q)$
representing
![]() $K$
.
$K$
.
Remark 2.16. Since the differential preserves the decomposition of the complex in
![]() $Spin^c$
structures (Proposition 2.11), we can write
$Spin^c$
structures (Proposition 2.11), we can write
and according to Proposition 2.11, the endomorphism
![]() $U$
induced in homology by any of the
$U$
induced in homology by any of the
![]() $V_i$
acts as
$V_i$
acts as
where
![]() $\mathrm{GH}^-_m (L(p,q),K,s,a)$
is the homology in tri-grading
$\mathrm{GH}^-_m (L(p,q),K,s,a)$
is the homology in tri-grading
![]() $(m,a,s) \in \left(\mathbb{Q},\mathbb{Q},\mathbb{Z}_p\right)$
.
$(m,a,s) \in \left(\mathbb{Q},\mathbb{Q},\mathbb{Z}_p\right)$
.
We can finally state the main result from [Reference Baker, Grigsby and Hedden2]:
Theorem 2.17. (Thm. 1.1 of [Reference Baker, Grigsby and Hedden2]) Let
![]() $G$
be a grid for a knot
$G$
be a grid for a knot
![]() $K \subset L(p,q)$
. There is a graded isomorphism of
$K \subset L(p,q)$
. There is a graded isomorphism of
![]() $\mathbb{F}[U]$
and, respectively,
$\mathbb{F}[U]$
and, respectively,
![]() $\mathbb{F}$
tri-graded modules:
$\mathbb{F}$
tri-graded modules:
Remark 2.18. Knot Floer homology is known (see e.g. [Reference Ozsváth and Szabó19, Thm. 7.1]) to satisfy a formulaFootnote 8 for the connected sum of two knots in rational homology 3-spheres; if
![]() $ (Y,K) = (Y_0,K_0)\#(Y_1,K_1)$
, then
$ (Y,K) = (Y_0,K_0)\#(Y_1,K_1)$
, then
In each connected 3-manifold
![]() $Y$
, the isotopy class of the homologically trivial unknot
$Y$
, the isotopy class of the homologically trivial unknot
![]() $\bigcirc$
is unique (since it bounds an embedded disk and manifolds are homogeneous); thus, we can think of a local knot
$\bigcirc$
is unique (since it bounds an embedded disk and manifolds are homogeneous); thus, we can think of a local knot
![]() $K$
, that is, a knot contained in a 3-ball inside
$K$
, that is, a knot contained in a 3-ball inside
![]() $Y$
as the connected sum
$Y$
as the connected sum
for some knot
![]() $K^\prime$
in
$K^\prime$
in
![]() $S^3$
. It is then a straightforward computation to show that the grid homology of the unknot
$S^3$
. It is then a straightforward computation to show that the grid homology of the unknot
![]() $\bigcirc \subset L(p,q)$
is:
$\bigcirc \subset L(p,q)$
is:
So, by equation (6)
In other words, the grid homology of a local knot is completely determined by the homology of the same knot viewed as living in
![]() $S^3$
(and in particular its Alexander degrees are integers).
$S^3$
(and in particular its Alexander degrees are integers).
Remark 2.19. A simple knot in
![]() $L(p,q)$
is a knot admitting a grid of dimension 1, (see also [Reference Hedden11] and [Reference Rasmussen25]). It is easy to show that in each lens space
$L(p,q)$
is a knot admitting a grid of dimension 1, (see also [Reference Hedden11] and [Reference Rasmussen25]). It is easy to show that in each lens space
![]() $L(p,q)$
, there is exactly one simple knot in each homology class; for
$L(p,q)$
, there is exactly one simple knot in each homology class; for
![]() $m \in \mathrm{H}_1 (L(p,q);\,\mathbb{Z})$
, denote this knot by
$m \in \mathrm{H}_1 (L(p,q);\,\mathbb{Z})$
, denote this knot by
![]() $T^{p,q}_m$
. If
$T^{p,q}_m$
. If
![]() $G$
is the dimension
$G$
is the dimension
![]() $1$
grid representing a simple knot in
$1$
grid representing a simple knot in
![]() $L(p,q)$
, then
$L(p,q)$
, then
![]() $|S(G)| = p$
, and there is exactly one generator in each
$|S(G)| = p$
, and there is exactly one generator in each
![]() $Spin^c$
degree. Therefore, there is no differential (since
$Spin^c$
degree. Therefore, there is no differential (since
![]() $\partial$
preserves the
$\partial$
preserves the
![]() $Spin^c$
degree), so the homologies of
$Spin^c$
degree), so the homologies of
![]() $T^{p,q}_m$
are as follows:
$T^{p,q}_m$
are as follows:
where
![]() $A(x_s)$
is the Alexander degree of the unique generators in degree
$A(x_s)$
is the Alexander degree of the unique generators in degree
![]() $s$
. As in [Reference Baker, Grigsby and Hedden2], we say that these knots are Floer simple (or
$s$
. As in [Reference Baker, Grigsby and Hedden2], we say that these knots are Floer simple (or
![]() $U$
-knot in the terminology of [Reference Ozsváth and Szabó18]), meaning that the rank of the grid homology (over the appropriate ground ring) is exactly one in each
$U$
-knot in the terminology of [Reference Ozsváth and Szabó18]), meaning that the rank of the grid homology (over the appropriate ground ring) is exactly one in each
![]() $Spin^c$
degree.
$Spin^c$
degree.
3. Lift to
 $\mathbb{Z}$
coefficients
$\mathbb{Z}$
coefficients
The complexes we have used until now were defined to work with
![]() $\mathbb{F}$
as base ring; in particular, the proof of Proposition 2.11 relied on the parity of polygon decompositions to ensure that
$\mathbb{F}$
as base ring; in particular, the proof of Proposition 2.11 relied on the parity of polygon decompositions to ensure that
![]() $ ( \mathrm{GC}^-, \partial )$
is in fact a chain complex. This section is devoted to prove Theorem 1.1, by exhibiting a combinatorial extension of the previous construction to integer coefficients. This was first done in the combinatorial setting for
$ ( \mathrm{GC}^-, \partial )$
is in fact a chain complex. This section is devoted to prove Theorem 1.1, by exhibiting a combinatorial extension of the previous construction to integer coefficients. This was first done in the combinatorial setting for
![]() $S^3$
in [Reference Manolescu, Ozsváth, Szabó and Thurston15] (see also [Reference Ozsváth, Stipsicz and Szabó17]).
$S^3$
in [Reference Manolescu, Ozsváth, Szabó and Thurston15] (see also [Reference Ozsváth, Stipsicz and Szabó17]).
We will adopt the group theoretic approach first developed in [Reference Gallais10] to define a sign function on rectangles, whose properties are precisely tuned to have
![]() $ \partial ^2=0$
. We note here that knot Floer homology can be defined in the analytic setting with integer coefficients [Reference Ozsváth and Szabó19], but it is currently not known whether it coincides with its combinatorial counterparts.
$ \partial ^2=0$
. We note here that knot Floer homology can be defined in the analytic setting with integer coefficients [Reference Ozsváth and Szabó19], but it is currently not known whether it coincides with its combinatorial counterparts.
A natural question to ask is to what extent the theory can change under such a change of coefficients; at the time of writing, there is no example of a knot in
![]() $S^3$
whose knot Floer homology with
$S^3$
whose knot Floer homology with
![]() $\mathbb{Z}$
coefficients exhibits torsion (see Problem 17.2.9 of [Reference Ozsváth, Stipsicz and Szabó22]). Even in the lens space case, the computations displayed in section 4 seem to suggest an analogous situation (see also the discussion in [Reference Ozsváth, Stipsicz and Szabó22, Sec. 15.6]).
$\mathbb{Z}$
coefficients exhibits torsion (see Problem 17.2.9 of [Reference Ozsváth, Stipsicz and Szabó22]). Even in the lens space case, the computations displayed in section 4 seem to suggest an analogous situation (see also the discussion in [Reference Ozsváth, Stipsicz and Szabó22, Sec. 15.6]).
It is convenient to define signs on
![]() $Rect(G)$
, rather than directly on
$Rect(G)$
, rather than directly on
![]() $Rect^\circ (G)$
; moreover, the signs will not depend on the choice of a knot, but just on the parameters of the grid.
$Rect^\circ (G)$
; moreover, the signs will not depend on the choice of a knot, but just on the parameters of the grid.
Definition 3.1.
Given a grid diagram
![]() $G$
, a sign assignment on
$G$
, a sign assignment on
![]() $G$
is a function
$G$
is a function
such that the following conditions hold:
-
1. If
 $r_1 \ast r_2 = r_3 \ast r_4$
then
$r_1 \ast r_2 = r_3 \ast r_4$
then
 $\mathcal{S}(r_1) \mathcal{S}(r_2) = - \mathcal{S}(r_3)\mathcal{S}(r_4)$
$\mathcal{S}(r_1) \mathcal{S}(r_2) = - \mathcal{S}(r_3)\mathcal{S}(r_4)$
-
2. If
 $r_1 \ast r_2$
is a horizontal annulus (
$r_1 \ast r_2$
is a horizontal annulus (
 $\alpha$
-strip), then
$\alpha$
-strip), then
 $\mathcal{S}(r_1)\mathcal{S}(r_2) = 1$
$\mathcal{S}(r_1)\mathcal{S}(r_2) = 1$
-
3. If
 $r_1 \ast r_2$
is a vertical annulus (
$r_1 \ast r_2$
is a vertical annulus (
 $\beta$
-strip), then
$\beta$
-strip), then
 $\mathcal{S}(r_1)\mathcal{S}(r_2) = -1$
$\mathcal{S}(r_1)\mathcal{S}(r_2) = -1$
We will prove in Theorem 3.7 that sign assignments actually exist on twisted grid diagrams and deal with problems related to their uniqueness later on.
We can now show how such a sign
![]() $\mathcal{S}$
can be used to promote
$\mathcal{S}$
can be used to promote
![]() $\widehat{\mathrm{GC}}(G)$
and
$\widehat{\mathrm{GC}}(G)$
and
![]() $ \mathrm{GC}^-(G)$
from
$ \mathrm{GC}^-(G)$
from
![]() $\mathbb{F} [ V_1, \ldots, V_n ]$
to
$\mathbb{F} [ V_1, \ldots, V_n ]$
to
![]() $\mathbb{Z} [ V_1, \ldots, V_n ]$
complexes.
$\mathbb{Z} [ V_1, \ldots, V_n ]$
complexes.
To see why the properties given in the previous definition are indeed the right ones, fix a sign assignment
![]() $\mathcal{S}$
for
$\mathcal{S}$
for
![]() $G$
and define
$G$
and define
 \begin{equation*}\partial_{\mathcal{S}} (x) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x, y)\\ r \cap \mathbb{X} = \emptyset}} \mathcal{S}(r) \left( \prod_{i=1}^{n} {V_i}^{O_i (r)} \right) y , \end{equation*}
\begin{equation*}\partial_{\mathcal{S}} (x) = \sum_{y \in S(G)} \sum_{\substack{r \in Rect^\circ (x, y)\\ r \cap \mathbb{X} = \emptyset}} \mathcal{S}(r) \left( \prod_{i=1}^{n} {V_i}^{O_i (r)} \right) y , \end{equation*}
Let us examine the coefficient of a generator
![]() $z \neq x$
in
$z \neq x$
in
![]() $ \partial _{\mathcal{S}}^2 (x)$
; each polygon connecting
$ \partial _{\mathcal{S}}^2 (x)$
; each polygon connecting
![]() $x$
to
$x$
to
![]() $z$
can be decomposed in two ways (as seen in Proposition 2.11). The pairs corresponding to inequivalent decompositions of the same polygon cancel out due to condition (1) on
$z$
can be decomposed in two ways (as seen in Proposition 2.11). The pairs corresponding to inequivalent decompositions of the same polygon cancel out due to condition (1) on
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
If instead
![]() $x = z$
, there are exactly
$x = z$
, there are exactly
![]() $2n$
possible ways of connecting a generator to itself with empty polygons, which are
$2n$
possible ways of connecting a generator to itself with empty polygons, which are
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
degenerations; as noted before, all of these strips contain one
$\beta$
degenerations; as noted before, all of these strips contain one
![]() $\mathbb{X}$
marking, so they do not contribute to the differential.
$\mathbb{X}$
marking, so they do not contribute to the differential.
In order to prove the existence of a sign assignment, we are going to adopt the approach used in [Reference Ozsváth, Stipsicz and Szabó22], which relies on the paper [Reference Gallais10] of Gallais regarding the so-called Spin extension of the permutation groups, introduced in the next definition.
Definition 3.2.
The Spin central extension of the symmetric group
![]() $\mathfrak{S}_n$
is the group
$\mathfrak{S}_n$
is the group
![]() $\widetilde{\mathfrak{S}}_n$
generated by the elements
$\widetilde{\mathfrak{S}}_n$
generated by the elements
subject to the following relations:
-
•
 $z^2 = 1\:$
and
$z^2 = 1\:$
and
 $\: z \widetilde{\tau }_{i,j} = \widetilde{\tau }_{i,j} z\:$
for
$\: z \widetilde{\tau }_{i,j} = \widetilde{\tau }_{i,j} z\:$
for
 $\:1 \le i \neq j \le n$
$\:1 \le i \neq j \le n$
-
•
 $ \widetilde{\tau }_{i,j}^2 =z\:$
and
$ \widetilde{\tau }_{i,j}^2 =z\:$
and
 $\:\widetilde{\tau }_{i,j} = z\widetilde{\tau }_{j,i}$
$\:\widetilde{\tau }_{i,j} = z\widetilde{\tau }_{j,i}$
-
•
 $ \widetilde{\tau }_{i,j} \widetilde{\tau }_{k,l} = z \widetilde{\tau }_{k,l} \widetilde{\tau }_{i,j} \:$
for distinct
$ \widetilde{\tau }_{i,j} \widetilde{\tau }_{k,l} = z \widetilde{\tau }_{k,l} \widetilde{\tau }_{i,j} \:$
for distinct
 $\:1 \le i,j,k,l \le n$
$\:1 \le i,j,k,l \le n$
-
•
 $\widetilde{\tau }_{i,j} \widetilde{\tau }_{j,k} \widetilde{\tau }_{i,j} = \widetilde{\tau }_{j,k} \widetilde{\tau }_{i,j} \widetilde{\tau }_{j,k} = \widetilde{\tau }_{i,k}\:$
for distinct
$\widetilde{\tau }_{i,j} \widetilde{\tau }_{j,k} \widetilde{\tau }_{i,j} = \widetilde{\tau }_{j,k} \widetilde{\tau }_{i,j} \widetilde{\tau }_{j,k} = \widetilde{\tau }_{i,k}\:$
for distinct
 $\:1 \le i,j,k \le n$
$\:1 \le i,j,k \le n$
Remark 3.3. The name Spin central extension is justified by the fact that this group can be derived as a
![]() ${\mathbb{Z}}/{2\mathbb{Z}}$
extension of
${\mathbb{Z}}/{2\mathbb{Z}}$
extension of
![]() $\mathfrak{S}_n$
induced by the short exact sequence
$\mathfrak{S}_n$
induced by the short exact sequence
Here,
![]() $\pi$
is the surjective homomorphism defined by
$\pi$
is the surjective homomorphism defined by
![]() $\pi (z) =1$
and
$\pi (z) =1$
and
![]() $\pi (\widetilde{\tau }_{i,j}) =\tau _{i,j}$
.
$\pi (\widetilde{\tau }_{i,j}) =\tau _{i,j}$
.
Definition 3.4.
A section for
![]() $\widetilde{\mathfrak{S}}_n$
is a map
$\widetilde{\mathfrak{S}}_n$
is a map
such that
![]() $\pi \circ \rho = \mathrm{Id}_{\mathfrak{S}_n}$
. We will make a slight notational abuse and also call sections the maps
$\pi \circ \rho = \mathrm{Id}_{\mathfrak{S}_n}$
. We will make a slight notational abuse and also call sections the maps
given by considering the product of a section with the identity map on
![]() $\mathbb{Z}_p^n$
.
$\mathbb{Z}_p^n$
.
We are going to define a map
that associates to a rectangle
![]() $r \in Rect(x,y)$
an element in
$r \in Rect(x,y)$
an element in
![]() $ \widetilde{\mathfrak{S}}_n \times \mathbb{Z}_p^n$
, enabling us to ‘compare’ the generators that compose the vertices of
$ \widetilde{\mathfrak{S}}_n \times \mathbb{Z}_p^n$
, enabling us to ‘compare’ the generators that compose the vertices of
![]() $r$
. If the elements of
$r$
. If the elements of
![]() $x$
and
$x$
and
![]() $y$
in the bottom edge of
$y$
in the bottom edge of
![]() $r$
belong, respectively, to
$r$
belong, respectively, to
![]() $\beta _i$
and
$\beta _i$
and
![]() $\beta _j$
, the first component of
$\beta _j$
, the first component of
![]() $\varphi (r)$
is given by the generalised transposition
$\varphi (r)$
is given by the generalised transposition
![]() $\widetilde{\tau }_{i,j}$
. The second component of
$\widetilde{\tau }_{i,j}$
. The second component of
![]() $\varphi$
is given by the difference between the
$\varphi$
is given by the difference between the
![]() $p$
-coordinates of
$p$
-coordinates of
![]() $x$
and
$x$
and
![]() $y$
. The two generators differ only in two components, so necessarily
$y$
. The two generators differ only in two components, so necessarily
for some
![]() $k \in \{0, \ldots, p-1\}$
.
$k \in \{0, \ldots, p-1\}$
.
Remark 3.5. To simplify the proof of the next theorem, we observe here that the generalised permutation part of the map
![]() $\varphi$
does not depend on the eventual ‘wrapping’ of a rectangle on the grid, while the
$\varphi$
does not depend on the eventual ‘wrapping’ of a rectangle on the grid, while the
![]() $\mathbb{Z}_p^n$
part does.
$\mathbb{Z}_p^n$
part does.
Example 3.6. Consider the rectangles
![]() $R$
in the left part of Figure 12; the value
$R$
in the left part of Figure 12; the value
![]() $\varphi (R)$
associated is
$\varphi (R)$
associated is
![]() $ ( \widetilde{\tau }_{1,3}, (0,-1,0,1,0) )$
for the horizontal one and
$ ( \widetilde{\tau }_{1,3}, (0,-1,0,1,0) )$
for the horizontal one and
![]() $ ( \widetilde{\tau }_{4,5}, (0,0,0,0) )$
for the vertical. Note also that swapping the order of the column’s indices changes the associated generalised transposition, as indicated in Figure 16.
$ ( \widetilde{\tau }_{4,5}, (0,0,0,0) )$
for the vertical. Note also that swapping the order of the column’s indices changes the associated generalised transposition, as indicated in Figure 16.

Figure 16. The generalised transpositions associated with these two rectangles are
![]() $\widetilde{\tau }_{ij}$
and
$\widetilde{\tau }_{ij}$
and
![]() $\widetilde{\tau }_{ji} = z\widetilde{\tau }_{ij}$
.
$\widetilde{\tau }_{ji} = z\widetilde{\tau }_{ij}$
.

Figure 17. An
![]() $\alpha$
-strip of height 1. Only the relevant components of the generators are shown.
$\alpha$
-strip of height 1. Only the relevant components of the generators are shown.
Given a section
![]() $\rho$
, we can build a sign assignment as follows:
$\rho$
, we can build a sign assignment as follows:
 \begin{equation}{\mathcal S}_\rho(r)=\left\{\begin{array}{r@{\quad}l}1&{\text{ if }}\rho(x)\varphi(r)=\rho(y)\\[4pt]-1&{\text{ if }}\rho(x)\varphi(r)=z\rho(y)\end{array}\right.,\end{equation}
\begin{equation}{\mathcal S}_\rho(r)=\left\{\begin{array}{r@{\quad}l}1&{\text{ if }}\rho(x)\varphi(r)=\rho(y)\\[4pt]-1&{\text{ if }}\rho(x)\varphi(r)=z\rho(y)\end{array}\right.,\end{equation}
for
![]() $r \in Rect(x,y)$
. The operation on
$r \in Rect(x,y)$
. The operation on
![]() $ \widetilde{\mathfrak{S}}_n \times \mathbb{Z}_p^n$
consists in the product of permutations on the first factor and addition on the
$ \widetilde{\mathfrak{S}}_n \times \mathbb{Z}_p^n$
consists in the product of permutations on the first factor and addition on the
![]() $p$
-coordinates.
$p$
-coordinates.
Theorem 3.7.
For any given section
![]() $\rho$
on
$\rho$
on
![]() $\widetilde{\mathfrak{S}}_n$
, the function
$\widetilde{\mathfrak{S}}_n$
, the function
![]() $ \mathcal{S}_\rho$
defined above is a sign assignment.
$ \mathcal{S}_\rho$
defined above is a sign assignment.
Proof. First, we deal with
![]() $\alpha$
-strips; suppose
$\alpha$
-strips; suppose
![]() $R_1 \in Rect(x,y)$
,
$R_1 \in Rect(x,y)$
,
![]() $R_2 \in Rect(y,x)$
are such that
$R_2 \in Rect(y,x)$
are such that
![]() $R_1*R_2$
is an
$R_1*R_2$
is an
![]() $\alpha$
-strip. Then, we have
$\alpha$
-strip. Then, we have
for some indices
![]() $i,j$
and integer
$i,j$
and integer
![]() $k$
.
$k$
.
So if
then
which implies
![]() $\mathcal{S}(R_1) = \mathcal{S}(R_1) = 1$
.
$\mathcal{S}(R_1) = \mathcal{S}(R_1) = 1$
.
If instead we had
then
In both cases,
![]() $\mathcal{S}(R_1) \mathcal{S}(R_2) = 1$
.
$\mathcal{S}(R_1) \mathcal{S}(R_2) = 1$
.
Next, we examine the behaviour of signs for
![]() $\beta$
-strips. As in the previous case, there is only one other possible generator
$\beta$
-strips. As in the previous case, there is only one other possible generator
![]() $y$
that induces a decomposition of an annulus starting from
$y$
that induces a decomposition of an annulus starting from
![]() $x$
. The permutation components of the two rectangles
$x$
. The permutation components of the two rectangles
![]() $R_1 \in Rect(x,y)$
and
$R_1 \in Rect(x,y)$
and
![]() $R_2 \in Rect(y,x)$
are both
$R_2 \in Rect(y,x)$
are both
![]() $\widetilde{\tau }_{i,j}$
. So if
$\widetilde{\tau }_{i,j}$
. So if
which implies
![]() $\mathcal{S}(R_1) \mathcal{S}(R_2) = -1$
.
$\mathcal{S}(R_1) \mathcal{S}(R_2) = -1$
.
The centrality of
![]() $z$
in
$z$
in
![]() $\widetilde{\mathfrak{S}}_n$
tells us that the case with
$\widetilde{\mathfrak{S}}_n$
tells us that the case with
![]() $\mathcal{S}(R_1) = -1$
is identical.
$\mathcal{S}(R_1) = -1$
is identical.
Now, given a general polygon
![]() $P = r*r^\prime$
connecting two generators
$P = r*r^\prime$
connecting two generators
![]() $x \neq x^\prime$
, we can easily prove that Definition 3.2 implies
$x \neq x^\prime$
, we can easily prove that Definition 3.2 implies
To show this, assume
![]() $r \in Rect(x,w)$
and
$r \in Rect(x,w)$
and
![]() $r' \in Rect(w,x')$
for some intermediate generator
$r' \in Rect(w,x')$
for some intermediate generator
![]() $w$
. Then, by equation (9), it is immediate to see that
$w$
. Then, by equation (9), it is immediate to see that
![]() $\varphi (r) \varphi (r') \rho (x)$
is equal to either
$\varphi (r) \varphi (r') \rho (x)$
is equal to either
![]() $\rho (w) \varphi (r')$
or
$\rho (w) \varphi (r')$
or
![]() $z\rho (w) \varphi (r')$
, according to whether
$z\rho (w) \varphi (r')$
, according to whether
![]() $\mathcal{S}(r) =1$
or
$\mathcal{S}(r) =1$
or
![]() $\mathcal{S}(r) = -1$
, respectively. In the same way,
$\mathcal{S}(r) = -1$
, respectively. In the same way,
![]() $\rho (w) \varphi (r')$
is equal to either
$\rho (w) \varphi (r')$
is equal to either
![]() $\rho (x')$
or
$\rho (x')$
or
![]() $z \rho (x')$
, this time according to the value of
$z \rho (x')$
, this time according to the value of
![]() $\mathcal{S}(r')$
. The factor
$\mathcal{S}(r')$
. The factor
![]() $z^{\frac{1 -\mathcal{S}(r) \mathcal{S}(r^\prime )}{2}}$
in equation (10) compensates the possible appearance of
$z^{\frac{1 -\mathcal{S}(r) \mathcal{S}(r^\prime )}{2}}$
in equation (10) compensates the possible appearance of
![]() $z$
factors.
$z$
factors.
According to the proof of Proposition 2.11, each polygon which is not an
![]() $\alpha/\beta$
-strip can be written as the concatenation of two distinct pairs of rectangles; so we just need to check for all possible polygons
$\alpha/\beta$
-strip can be written as the concatenation of two distinct pairs of rectangles; so we just need to check for all possible polygons
that the following identity holds:
where
![]() $y\neq w$
are two auxiliary generators which differ by only one transposition from
$y\neq w$
are two auxiliary generators which differ by only one transposition from
![]() $x$
and
$x$
and
![]() $z$
. All we need to do is verify equation (11) in the cases
$z$
. All we need to do is verify equation (11) in the cases
![]() $M = 2,3,4$
from the proof of Proposition 2.11 (recall that we already considered
$M = 2,3,4$
from the proof of Proposition 2.11 (recall that we already considered
![]() $M=0$
, and
$M=0$
, and
![]() $M=1$
was discarded).
$M=1$
was discarded).
It is easy to check that the generalised permutations associated with polygons corresponding to the
![]() $M=3$
case are the same of [Reference Ozsváth, Stipsicz and Szabó22, Ch. 15] in the
$M=3$
case are the same of [Reference Ozsváth, Stipsicz and Szabó22, Ch. 15] in the
![]() $S^3$
case; in particular, this is true even when the rectangles wrap around the grid (see Figure 20), since the generalised permutation part does not depend on the
$S^3$
case; in particular, this is true even when the rectangles wrap around the grid (see Figure 20), since the generalised permutation part does not depend on the
![]() $p$
-coordinates of the generators.
$p$
-coordinates of the generators.
The case
![]() $M=4$
is immediate: as shown in Figure 18
$M=4$
is immediate: as shown in Figure 18

Figure 18. The generalised permutations associated with the green and blue rectangles are
![]() $\widetilde{\tau }_{ij}$
and
$\widetilde{\tau }_{ij}$
and
![]() $\widetilde{\tau }_{kl}$
, respectively.
$\widetilde{\tau }_{kl}$
, respectively.
The permutations associated with the two decompositions are such that equation (11) becomes exactly the third relation defining
![]() $\widetilde{\mathfrak{S}}_n$
.
$\widetilde{\mathfrak{S}}_n$
.
Lastly, we deal with
![]() $M=2$
; the generalised transpositions associated with
$M=2$
; the generalised transpositions associated with
![]() $r(x,y)$
and
$r(x,y)$
and
![]() $r(y,x^\prime )$
are
$r(y,x^\prime )$
are
![]() $\widetilde{\tau }_{ij}$
and
$\widetilde{\tau }_{ij}$
and
![]() $\widetilde{\tau }_{ji}$
. For the two rectangles
$\widetilde{\tau }_{ji}$
. For the two rectangles
![]() $r(x,w)$
and
$r(x,w)$
and
![]() $r(w,x^\prime )$
on the right in Figure 19, the associated transposition is
$r(w,x^\prime )$
on the right in Figure 19, the associated transposition is
![]() $\widetilde{\tau }_{ij}$
in both cases. So in particular, this implies that if
$\widetilde{\tau }_{ij}$
in both cases. So in particular, this implies that if
![]() $\mathcal{S}(r(x,y))\mathcal{S}(r(y,x^\prime )) =-1$
then
$\mathcal{S}(r(x,y))\mathcal{S}(r(y,x^\prime )) =-1$
then
![]() $\mathcal{S}(r(x,w))\mathcal{S}(r(w,x^\prime )) =1$
and vice versa. Therefore, equation (11) is always satisfied, and we are done.
$\mathcal{S}(r(x,w))\mathcal{S}(r(w,x^\prime )) =1$
and vice versa. Therefore, equation (11) is always satisfied, and we are done.

Figure 19. The generalised transpositions
![]() $\widetilde{\tau }_{ij}$
and
$\widetilde{\tau }_{ij}$
and
![]() $\widetilde{\tau }_{ji}$
are associated with the two decompositions in the
$\widetilde{\tau }_{ji}$
are associated with the two decompositions in the
![]() $M=2$
case.
$M=2$
case.

Figure 20. The four relevant combinatorial possibilities for the
![]() $M=3$
case in the
$M=3$
case in the
![]() $S^3$
setting. Remember that the eventual wrapping of one rectangle over the other does not change the relations in
$S^3$
setting. Remember that the eventual wrapping of one rectangle over the other does not change the relations in
![]() $\widetilde{\mathfrak{S}}_n$
.
$\widetilde{\mathfrak{S}}_n$
.
Remark 3.8. It is worth noting that the trivial choice for signs – that is, treating each rectangle just as a generalised permutation, without keeping track of
![]() $p$
-coordinates (like in the
$p$
-coordinates (like in the
![]() $S^3$
setting) – cannot distinguish a
$S^3$
setting) – cannot distinguish a
![]() $\beta$
degeneration from other polygons which admit two distinct decompositions into rectangles, as shown in Figure 21.
$\beta$
degeneration from other polygons which admit two distinct decompositions into rectangles, as shown in Figure 21.

Figure 21. The white and black generators have the same permutation component, but the polygon connecting them admits two distinct decompositions. In particular, it cannot be an
![]() $\alpha/\beta$
-strip.
$\alpha/\beta$
-strip.
Definition 3.9.
A section
![]() $\rho \,:\, \mathfrak{S}_n \times \mathbb{Z}_p^n \longrightarrow \widetilde{\mathfrak{S}}_n \times \mathbb{Z}_p^n$
is said to be compatible with a sign assignment
$\rho \,:\, \mathfrak{S}_n \times \mathbb{Z}_p^n \longrightarrow \widetilde{\mathfrak{S}}_n \times \mathbb{Z}_p^n$
is said to be compatible with a sign assignment
![]() $\mathcal{S}$
if for any pair
$\mathcal{S}$
if for any pair
![]() $x,y$
of generators, and any
$x,y$
of generators, and any
![]() $r \in Rect(x,y)$
$r \in Rect(x,y)$
 \begin{equation*}\rho(y)=\left\{\begin{array}{r@{\quad}l}\rho(x)\widetilde\tau(r)&{if}\ \mathcal S(r)=1\\[4pt]z\rho(x)\widetilde\tau(r)& if\ \mathcal S(r)=-1\end{array}\right.,\end{equation*}
\begin{equation*}\rho(y)=\left\{\begin{array}{r@{\quad}l}\rho(x)\widetilde\tau(r)&{if}\ \mathcal S(r)=1\\[4pt]z\rho(x)\widetilde\tau(r)& if\ \mathcal S(r)=-1\end{array}\right.,\end{equation*}
is satisfied.
Proposition 3.10.
Given a sign assignment
![]() $\mathcal{S}$
, there are exactly two compatible sections.
$\mathcal{S}$
, there are exactly two compatible sections.
Proof. Sections were defined in Definition 3.4 to be extensions of algebraic sections of the short exact sequence (7) via the identity on the
![]() $\mathbb{Z}_p^n$
component (for a grid of dimension
$\mathbb{Z}_p^n$
component (for a grid of dimension
![]() $n$
). Therefore, the statement is equivalent to proving the existence of exactly two compatible sections
$n$
). Therefore, the statement is equivalent to proving the existence of exactly two compatible sections
![]() $\rho \,:\, \mathfrak{S}_n \longrightarrow \widetilde{\mathfrak{S}}_n$
. This is precisely the content of [Reference Ozsváth, Stipsicz and Szabó22, Prop 15.2.13], so we can conclude.
$\rho \,:\, \mathfrak{S}_n \longrightarrow \widetilde{\mathfrak{S}}_n$
. This is precisely the content of [Reference Ozsváth, Stipsicz and Szabó22, Prop 15.2.13], so we can conclude.
Now, for the uniqueness of sign assignments, denote by
![]() $\mathcal{G}auge(G)$
the group of maps
$\mathcal{G}auge(G)$
the group of maps
![]() $\mathcal{G}auge(G)$
acts on sections as follows:
$\mathcal{G}auge(G)$
acts on sections as follows:
 \begin{equation}\rho^v(x)=\left\{\begin{array}{r@{\quad}l}\rho(x)&{\text{ if }}v(x)=1\\[4pt]z\rho(x)&{\text{ if }}v(x)=-1\end{array}\right.\!.\end{equation}
\begin{equation}\rho^v(x)=\left\{\begin{array}{r@{\quad}l}\rho(x)&{\text{ if }}v(x)=1\\[4pt]z\rho(x)&{\text{ if }}v(x)=-1\end{array}\right.\!.\end{equation}
This action is free and transitive;
![]() $\mathcal{G}auge(G)$
also acts on the set of sign assignments: if
$\mathcal{G}auge(G)$
also acts on the set of sign assignments: if
![]() $S$
is a sign on a grid
$S$
is a sign on a grid
![]() $G$
and
$G$
and
![]() $v \in \mathcal{G}auge(G)$
, define
$v \in \mathcal{G}auge(G)$
, define
![]() $S^v (r) = v(x) S(r) v(y)$
for
$S^v (r) = v(x) S(r) v(y)$
for
![]() $r \in Rect(x,y)$
.
$r \in Rect(x,y)$
.
As in the
![]() $S^3$
case, it is easy to show that there is only one sign assignment on a grid, up to this action of
$S^3$
case, it is easy to show that there is only one sign assignment on a grid, up to this action of
![]() $\mathcal{G}auge(G)$
. The uniqueness now follows by noting that if
$\mathcal{G}auge(G)$
. The uniqueness now follows by noting that if
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are two sign assignments on a grid
$S_2$
are two sign assignments on a grid
![]() $G$
, then
$G$
, then
![]() $S_2 = S_1^v$
for some
$S_2 = S_1^v$
for some
![]() $v \in \mathcal{G}auge(G)$
, and the map
$v \in \mathcal{G}auge(G)$
, and the map
given by
![]() $f(x) = v(x) x$
is an isomorphism (of tri-graded
$f(x) = v(x) x$
is an isomorphism (of tri-graded
![]() $R$
-modules). This concludes the proof of Theorem 1.1.
$R$
-modules). This concludes the proof of Theorem 1.1.
4. Computations
4.1. The programmes
It becomes immediately apparent that the work needed to actually compute
![]() $\widehat{\mathrm{GH}} (G)$
for grids with dimension greater than 3 is not manageable by hand.Footnote 9 So the author developed several programmes in Sage [27] capable of computing the hat flavoured grid homology of links in lens spaces. The computation can be made with
$\widehat{\mathrm{GH}} (G)$
for grids with dimension greater than 3 is not manageable by hand.Footnote 9 So the author developed several programmes in Sage [27] capable of computing the hat flavoured grid homology of links in lens spaces. The computation can be made with
![]() $\mathbb{Z}$
coefficients, provided that the grid dimension is less than 5.
$\mathbb{Z}$
coefficients, provided that the grid dimension is less than 5.
By using this tool, we were able to verify that all knots with a grid representative whose parameters satisfy the following conditions are
![]() $r$
-torsion-free (
$r$
-torsion-free (
![]() $r\le 17$
):
$r\le 17$
):
-
• for
 $n = 2$
,
$n = 2$
,
 $p \le 12$
$p \le 12$
-
• for
 $n= 3$
,
$n= 3$
,
 $p \le 6$
$p \le 6$
-
• for
 $n = 4$
,
$n = 4$
,
 $p \le 4$
$p \le 4$
-
•
 $n = 5$
,
$n = 5$
,
 $p\le 2$
$p\le 2$
The programmes can be freely used interactively online at my homepage [Reference Celoria4] or downloaded and used on a local Sage distribution. We recall here that there are several programmes that compute the grid homology/knot Floer homology of knots in the
![]() $3$
-sphere. In particular, M. Culler’s Gridlink [Reference Culler7] includes code by J.A. Baldwin and W.D. Gillam [Reference Baldwin and Gillam3] that computes
$3$
-sphere. In particular, M. Culler’s Gridlink [Reference Culler7] includes code by J.A. Baldwin and W.D. Gillam [Reference Baldwin and Gillam3] that computes
![]() $\widehat{\mathrm{GH}}$
, and there is a more recent programme by Ozsváth and Szabó [Reference Ozsváth and Szabó23] that can quickly compute
$\widehat{\mathrm{GH}}$
, and there is a more recent programme by Ozsváth and Szabó [Reference Ozsváth and Szabó23] that can quickly compute
![]() $\widehat{\mathrm{HFK}}$
for knots with relatively high crossing number.
$\widehat{\mathrm{HFK}}$
for knots with relatively high crossing number.
4.2. Grid homology calculator
The input consists of the grid parameters
![]() $(n,p,q)$
, followed by two strings of length
$(n,p,q)$
, followed by two strings of length
![]() $n$
determining the positions of the
$n$
determining the positions of the
![]() $\mathbb{X}$
and
$\mathbb{X}$
and
![]() $\mathbb{O}$
markings. We encode the markings with a string of length
$\mathbb{O}$
markings. We encode the markings with a string of length
![]() $n$
for each kind; to the
$n$
for each kind; to the
![]() $i$
-th marking (from the bottom row), we associate the number of the small square containing it (from the left, and starting from 0). As an example, the knot in Figure 2 is encoded as
$i$
-th marking (from the bottom row), we associate the number of the small square containing it (from the left, and starting from 0). As an example, the knot in Figure 2 is encoded as
![]() $\mathbb{X} = [12, 1,8,5,9]$
and
$\mathbb{X} = [12, 1,8,5,9]$
and
![]() $ \mathbb{O} = [6,3,0,9,12]$
.
$ \mathbb{O} = [6,3,0,9,12]$
.
The output consists of the following:
-
• (Optional) A drawing of the chosen grid
-
• The hat grid homologyFootnote 10
 $\widehat{\mathrm{GH}}( G, \mathfrak{s};\,\mathbb{Z})$
for each
$\widehat{\mathrm{GH}}( G, \mathfrak{s};\,\mathbb{Z})$
for each
 $\mathfrak{s} \in Spin^c$
structure and its decategorification.
$\mathfrak{s} \in Spin^c$
structure and its decategorification. -
• Whether the knot is rationally fibred, the homology class and its rational genus (see [Reference Ni and Wu16, Sec. 1] for the definitions).
-
• (Optional) A long list of the generators with their bi-grading.
-
• (Optional) A drawing of the grid for the lift of the knot to
 $S^3$
, together with its (univariate) Alexander polynomial and the number of components of the lift.
$S^3$
, together with its (univariate) Alexander polynomial and the number of components of the lift.
Basically, the programme creates the generators
![]() $S(G)$
and computes their degrees; afterwards, it checks for empty rectangles and creates the matrices of the differentials.
$S(G)$
and computes their degrees; afterwards, it checks for empty rectangles and creates the matrices of the differentials.
Rather than computing the module
![]() $\widehat{\mathrm{GC}} (G)$
, we adopt the simpler approach of computing yet another version of the grid homology, known as tilde flavoured homology,
$\widehat{\mathrm{GC}} (G)$
, we adopt the simpler approach of computing yet another version of the grid homology, known as tilde flavoured homology,
![]() $\widetilde{\mathrm{GH}}(G)$
.
$\widetilde{\mathrm{GH}}(G)$
.
The complex is simply the free
![]() $\mathbb{Z}$
module generated over
$\mathbb{Z}$
module generated over
![]() $S(G)$
, and the differential counts only those empty rectangles that do not contain any marking:
$S(G)$
, and the differential counts only those empty rectangles that do not contain any marking:
where
![]() $\mathcal{S}$
is a sign assignment.
$\mathcal{S}$
is a sign assignment.
Using the handy group theoretic capabilities of Sage, the relations in
![]() $\widetilde{\mathfrak{S}}_n$
(for
$\widetilde{\mathfrak{S}}_n$
(for
![]() $n \le 5$
) were encoded in a matrix associated with the differential.
$n \le 5$
) were encoded in a matrix associated with the differential.
A minor technical hurdle here is represented by the fact that the tilde flavoured version is not directly an invariant of the knot represented by the grid. This can be easily seen, for example, by computing
![]() $\widetilde{\mathrm{GH}} (G)$
in any
$\widetilde{\mathrm{GH}} (G)$
in any
![]() $Spin^c$
degree, for the grids of Example 2.9. However, the hat version can nonetheless be recovered from it:
$Spin^c$
degree, for the grids of Example 2.9. However, the hat version can nonetheless be recovered from it:
Proposition 4.1. (Prop. 4.6.13 of [Reference Ozsváth, Stipsicz and Szabó22]) Given a grid
![]() $G$
of dimension
$G$
of dimension
![]() $n$
representing the knot
$n$
representing the knot
![]() $K \subset L(p,q)$
, there is a graded isomorphism
$K \subset L(p,q)$
, there is a graded isomorphism
where
![]() $W = \mathbb{Z}_{[0,0]} \oplus \mathbb{Z}_{[-1,-1]}$
.
$W = \mathbb{Z}_{[0,0]} \oplus \mathbb{Z}_{[-1,-1]}$
.
After computing the homology
![]() $\widetilde{\mathrm{GH}}(G)$
, the programme ‘factors out’ the tensor product dependent on the size of the grid and prints the requested information.
$\widetilde{\mathrm{GH}}(G)$
, the programme ‘factors out’ the tensor product dependent on the size of the grid and prints the requested information.
4.3. A small example
Knot theory (and hence grid homology) in lens spaces is quite more complex than its 3-sphere counterpart: besides the fact that knots need not be homologically trivial, they also can be non-trivial for very small grid parameters. As an example, define
Then,
![]() $f(1) = 5$
(this is the trefoil in
$f(1) = 5$
(this is the trefoil in
![]() $S^3$
),
$S^3$
),
![]() $f(2) = 3$
and
$f(2) = 3$
and
![]() $f(p\gt 2) = 2$
(for this last case see Figure 22).
$f(p\gt 2) = 2$
(for this last case see Figure 22).

Figure 22. The knot in
![]() $L(3,1)$
described by
$L(3,1)$
described by
![]() $\mathbb{X},\mathbb{O} = [0,1], [3,4]$
.
$\mathbb{X},\mathbb{O} = [0,1], [3,4]$
.
Example 4.2. We sketch here the computation for the various flavours of grid homology in the case of the knot in Figure 22. The generating set
![]() $S(G,s)$
in each
$S(G,s)$
in each
![]() $Spin^c$
degree
$Spin^c$
degree
![]() $s \in \{0,\pm 1\}$
has 6 elements, which we will denote
$s \in \{0,\pm 1\}$
has 6 elements, which we will denote
![]() $x^0_s, \ldots, x^5_s$
for
$x^0_s, \ldots, x^5_s$
for
![]() $s = 0,1$
. We do not need to compute the
$s = 0,1$
. We do not need to compute the
![]() $s = -1$
complex, as this is quasi-isomorphic to the
$s = -1$
complex, as this is quasi-isomorphic to the
![]() $s=1$
one (this follows from the existence of an involutive operation on the set of
$s=1$
one (this follows from the existence of an involutive operation on the set of
![]() $Spin^c$
structures, see for example [Reference Ozsváth and Szabó19, Sec. 3] for a detailed account).
$Spin^c$
structures, see for example [Reference Ozsváth and Szabó19, Sec. 3] for a detailed account).
We can now list the generators, with their bi-degree and differential:


Figure 23. The complexes
![]() $\widetilde{GC}(G, i)$
(on the left) and
$\widetilde{GC}(G, i)$
(on the left) and
![]() $\mathrm{GC}^- (G, i)$
(on the right) for
$\mathrm{GC}^- (G, i)$
(on the right) for
![]() $i = 0,1$
. Red dashed lines denote multiplication by
$i = 0,1$
. Red dashed lines denote multiplication by
![]() $V_1$
, while blue dotted lines denote multiplication by
$V_1$
, while blue dotted lines denote multiplication by
![]() $V_2$
.
$V_2$
.
Since
![]() $\widetilde{\mathrm{GC}}(G, 0)$
has no differentials,Footnote 11 the homology coincides with the complex. In
$\widetilde{\mathrm{GC}}(G, 0)$
has no differentials,Footnote 11 the homology coincides with the complex. In
![]() $Spin^c$
degree 1 instead, the tilde homology is generated by
$Spin^c$
degree 1 instead, the tilde homology is generated by
![]() $x_1^1$
and
$x_1^1$
and
![]() $x_1^4$
, so
$x_1^4$
, so
![]() $\widetilde{\mathrm{GH}}(G, 1) \cong \mathbb{Z}_{\left [\frac{1}{6},0 \right ]} \oplus \mathbb{Z}_{\left [-\frac{5}{6},-1 \right ]}$
.
$\widetilde{\mathrm{GH}}(G, 1) \cong \mathbb{Z}_{\left [\frac{1}{6},0 \right ]} \oplus \mathbb{Z}_{\left [-\frac{5}{6},-1 \right ]}$
.
The computation of the minus flavour is just slightly more involved;
![]() $\mathrm{GH}^- (L(3,1), K, 0)$
is composed by a copy of
$\mathrm{GH}^- (L(3,1), K, 0)$
is composed by a copy of
![]() $\mathbb{Z} [U ]$
generated by
$\mathbb{Z} [U ]$
generated by
![]() $x_0^0$
, plus two
$x_0^0$
, plus two
![]() $U$
-torsion components, generated by
$U$
-torsion components, generated by
![]() $x_0^1 + x_0^2$
and
$x_0^1 + x_0^2$
and
![]() $x_0^3 + x_0^4$
. Altogether
$x_0^3 + x_0^4$
. Altogether
In the last case, we get
generated by
![]() $x_1^1$
. The hat homology can be obtained either by factoring out the tensor product with
$x_1^1$
. The hat homology can be obtained either by factoring out the tensor product with
![]() $\mathbb{Z}_{ [ 0,0 ]} \oplus \mathbb{Z}_{ [-1,-1 ]}$
from the tilde flavour or deleting all dotted differentials in the minus complex of Figure 23, then computing the homology.
$\mathbb{Z}_{ [ 0,0 ]} \oplus \mathbb{Z}_{ [-1,-1 ]}$
from the tilde flavour or deleting all dotted differentials in the minus complex of Figure 23, then computing the homology.
This particular knot is interesting for several reasons: firstly, it is the smallest non-trivial or simple knot in any lens space. More importantly, it can be also proved that, despite being null-homologous, it is not concordant (or even almost concordant, see [Reference Celoria5]) to a local knot. Finally, the group
![]() $\mathrm{GH}^-(G,0)$
is isomorphic (up to a shift in the Maslov grading) to the knot Floer homology of the trefoil knot in
$\mathrm{GH}^-(G,0)$
is isomorphic (up to a shift in the Maslov grading) to the knot Floer homology of the trefoil knot in
![]() $S^3$
; this in no accident and a rather more general statement is [Reference Alfieri, Celoria and Stipsicz1, Thm. 1.2].
$S^3$
; this in no accident and a rather more general statement is [Reference Alfieri, Celoria and Stipsicz1, Thm. 1.2].
Acknowledgment
I would like to thank my advisor Paolo Lisca and András Stipsicz for suggesting this topic, Paolo Aceto, Marco Golla, Enrico Manfredi, Francesco Lin and Agnese Barbensi for useful and interesting conversations and support. I would also like to thank the University of Pisa for the hospitality and the computational resources provided. Finally, I want to thank the referee for their detailed comments that helped to substantially improve the manuscript.