Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-02T23:38:28.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on a conjecture of Coxeter

Published online by Cambridge University Press:  18 May 2009

John Leech  and
Jens Mennicke
John Leech
Affiliation:
The University, Glasgow
Jens Mennicke
Affiliation:
The University, Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Coxeter [1] has studied groups defined by the relations

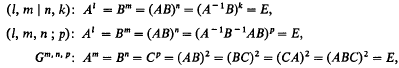
and gives lists of finite groups known to be completely defined by such sets of relations. In a later paper [2] he shows that G3, n, p is finite if n, p are both even and satisfy

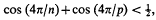
and expresses the conjecture that the restriction to even values may be removed. The only case satisfying this inequality and not already known to be finite is G3, 7, 16. In this note we show that G3, 7, 16 is indeed finite, being of order 21504 = 210.3.7, by showing that its subgroup

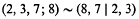
of index 2 is finite and of order 10752. Thus we add one entry to each of the lists of finite groups in Coxeter [1].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 5 , Issue 1 , January 1961 , pp. 25 - 29
Copyright
Copyright © Glasgow Mathematical Journal Trust 1961

References

1.Coxeter, H. S. M., The abstract groups Gm, n, p, Trans. Amer. Math. Soc. 45 (1939), 73–150.Google Scholar
2.Coxeter, H. S. M., Groups generated by unitary reflections of period 2, Canad. J. Math. 9 (1957), 243–272.CrossRefGoogle Scholar
3.Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete groups (Ergebnisse d. Math. N.F. 14, Springer, 1957).CrossRefGoogle Scholar
4.Sinkov, A., On the group-defining relations (2, 3, 7; q), Ann. Math. (2) 38 (1937), 577–584.CrossRefGoogle Scholar