Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1975.
Discrete-Parameter Martingales.
Vol. 10,
Issue. ,
p.
222.
Blake, Louis H.
1979.
Convergent processes, projective systems of measures and martingale decompositions.
Glasgow Mathematical Journal,
Vol. 20,
Issue. 2,
p.
119.
Blake, Louis H.
1981.
Tempered processes and a Riesz decomposition for some martingales in the limit.
Glasgow Mathematical Journal,
Vol. 22,
Issue. 1,
p.
9.
Gut, Allan
and
Schmidt, Klaus D.
1983.
Amarts and Set Function Processes.
Vol. 1042,
Issue. ,
p.
238.


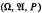 be a probability space with
be a probability space with 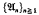 an increasing sequence of sub σ-fields of
an increasing sequence of sub σ-fields of 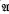 whose union generates
whose union generates 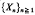 be a sequence of random variables adapted to
be a sequence of random variables adapted to  will be said to become fairer with time if, for every ε > ε,
will be said to become fairer with time if, for every ε > ε,