Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-26T03:16:50.526Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal radicals and normal classes of modules

Published online by Cambridge University Press:  18 May 2009

W. K. Nicholson  and
J. F. Watters
W. K. Nicholson
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, Canada T2N 1N4
J. F. Watters
Affiliation:
Department of Mathematics, The University of Leicester, Leicester, England LE1 7RH
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The study of special radicals was begun by Andrunakievič [1]. A class 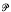of prime rings is called special if it is hereditary and closed under prime extensions. The upper radicals determined by special classes are called special. In later works Andrunakievič and Rjabuhin [2] and [3] defined the concept of a special class of modules.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 30 , Issue 1 , January 1988 , pp. 97 - 100
Copyright
Copyright © Glasgow Mathematical Journal Trust 1988

References

1.Andrunakievič, V. A., Radicals of associative rings. II. Examples of special radicals, Mat. Sb. (N.S.) 55 (97) (1961), 329–346; Amer. Math. Soc. Transl. (2) 52 (1966), 129–150.Google Scholar
2.Andrunakievič, V. A. and Rjabuhin, Ju. M., Special modules and special radicals, Dokl. Akad. Nauk SSSR 147 (1962), 1274–1277.Google Scholar
3.Andrunakievič, V. A. and Rjabuhin, Ju. M., Special modules and special radicals, In Memoriam: N. G. Čebotarev, 7–17, Izdat. Kazan. Univ., Kazan, 1964.Google Scholar
4.Desale, G. and Nicholson, W. K., Endoprimitive rings, J. Algebra 70 (1981), 548–560.CrossRefGoogle Scholar
5.Nicholson, W. K. and Watters, J. F., Normal radicals and normal classes of rings, J. Algebra 59 (1979), 5–15.CrossRefGoogle Scholar