Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-03T00:33:58.547Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal operators on Banach spaces

Published online by Cambridge University Press:  18 May 2009

Che-Kao Fong
Che-Kao Fong
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada M5S-IAI
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A (bounded, linear) operator H on a Banach space 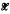is said to be hermitian if ∥exp(itH)∥ = 1 for all real t. An operator N on 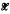is said to be normal if N = H + iK, where H and K are commuting hermitian operators. These definitions generalize those familiar concepts of operators on Hilbert spaces. Also, the normal derivations defined in [1] are normal operators. For more details about hermitian operators and normal operators on general Banach spaces, see [4]. The main result concerning normal operators in the present paper is the following theorem.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 20 , Issue 2 , July 1979 , pp. 163 - 168
Copyright
Copyright © Glasgow Mathematical Journal Trust 1979

References

REFERENCES

1.Anderson, J., On normal derivations. Proc. Amer. Math. Soc. 38 (1973), 135–140.CrossRefGoogle Scholar
2.Anderson, J. and Foias, C., Properties which normal operators share with normal derivations and related operators. Pacific J. Math. 61 (1975), 313–325.CrossRefGoogle Scholar
3.Berkson, E., Dowson, H. R. and Elliott, G. A., On Fuglede's theorem and scalar type operators. Bull. London Math. Soc. 4 (1972), 13–16.CrossRefGoogle Scholar
4.Bonsall, F. F. and Duncan, J., Numerical ranges of operators on normed spaces and of elements of normed algebras, London Math. Soc. Lecture Note Series No. 2, (Cambridge, 1971).CrossRefGoogle Scholar
5.Bonsall, F. F. and Duncan, J., Numerical ranges II, London Math. Soc. Lecture Note Series No. 10, (Cambridge, 1973).CrossRefGoogle Scholar
6.Choi, M. D. and Davis, C., The spectral mapping theorem for joint approximate point spectrum. Bull. Amer. Math. Soc. 80 (1974), 317–321.CrossRefGoogle Scholar
7.Crabb, M. J. and Spain, P. G., Commutators and normal operators, Glasgow Math. J. 18 (1977), 197–198.CrossRefGoogle Scholar
8.Rosenblum, M., On the operator equation BX - XA = Q. Duke Math. J. 23 (1956) 263–269.CrossRefGoogle Scholar
9.Sinclair, A. M., Eigenvalues in the boundary of the numerical range, Pacific J. Math. 35 (1970), 231–234.CrossRefGoogle Scholar