Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhou, Sizhong
2011.
A sufficient condition for graphs to be fractional (k,m)-deleted graphs.
Applied Mathematics Letters,
Vol. 24,
Issue. 9,
p.
1533.
ZHOU, SIZHONG
BIAN, QIUXIANG
and
XU, LAN
2012.
BINDING NUMBER AND MINIMUM DEGREE FOR FRACTIONAL (k,m)-DELETED GRAPHS.
Bulletin of the Australian Mathematical Society,
Vol. 85,
Issue. 1,
p.
60.
Zhou, Sizhong
2012.
A new neighborhood condition for graphs to be fractional (k,m)-deleted graphs.
Applied Mathematics Letters,
Vol. 25,
Issue. 3,
p.
509.
Zhou, Sizhong
Sun, Zhiren
and
Ye, Hui
2013.
A toughness condition for fractional -deleted graphs.
Information Processing Letters,
Vol. 113,
Issue. 8,
p.
255.
Gao, Wei
Guirao, Juan L. G.
and
Chen, Yao Jun
2019.
A Toughness Condition for Fractional (k, m)-deleted Graphs Revisited.
Acta Mathematica Sinica, English Series,
Vol. 35,
Issue. 7,
p.
1227.
Gao, Wei
Wang, Wei-fan
and
Chen, Yao-jun
2025.
Sharp Isolated Toughness Bound for Fractional (k, m)-Deleted Graphs.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 41,
Issue. 1,
p.
252.


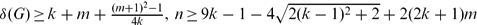 and
and 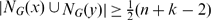 for each pair of non-adjacent vertices
for each pair of non-adjacent vertices 