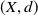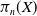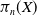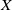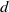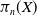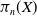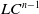1. Introduction
There are many ways to enrich the
![]() $n$
-th homotopy group
$n$
-th homotopy group
![]() $\pi _n(X,x_0)$
of a based topological space
$\pi _n(X,x_0)$
of a based topological space
![]() $(X,x_0)$
with a geometric or topological structure that remembers local features of the space
$(X,x_0)$
with a geometric or topological structure that remembers local features of the space
![]() $X$
, which are “unseen” by the usual group-theoretic structure, for example, the natural quotient topology [Reference Brazas and Fabel11], the
$X$
, which are “unseen” by the usual group-theoretic structure, for example, the natural quotient topology [Reference Brazas and Fabel11], the
![]() $\tau$
-topology [Reference Brazas9], the Spanier topology [Reference Abdullahi Rashid, Jamali, Mashayekhy, Pashaei and Torabi1, Reference Aceti and Brazas3], the whisker topology [Reference Abdullahi Rashid, Pashaei, Mashayekhy and Torabi2], and variations on these (e.g. coreflections in a convenient category). Of particular interest is the initial topology on
$\tau$
-topology [Reference Brazas9], the Spanier topology [Reference Abdullahi Rashid, Jamali, Mashayekhy, Pashaei and Torabi1, Reference Aceti and Brazas3], the whisker topology [Reference Abdullahi Rashid, Pashaei, Mashayekhy and Torabi2], and variations on these (e.g. coreflections in a convenient category). Of particular interest is the initial topology on
![]() $\pi _n(X,x_0)$
with respect to the canonical homomorphism
$\pi _n(X,x_0)$
with respect to the canonical homomorphism
![]() $\Psi _{n}\;:\;\pi _{n}(X,x_0)\to \check{\pi }_{n}(X,x_0)$
to the
$\Psi _{n}\;:\;\pi _{n}(X,x_0)\to \check{\pi }_{n}(X,x_0)$
to the
![]() $n$
-th shape homotopy group. This topology is often referred to as the shape topology and we denote the resulting topological group as
$n$
-th shape homotopy group. This topology is often referred to as the shape topology and we denote the resulting topological group as
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
. The shape topology gives
$\pi _{n}^{\text{sh}}(X,x_0)$
. The shape topology gives
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
the structure of a pro-discrete group and is closely related to Dugundji’s pre-shape-theory approach in [Reference Dugundji16]. While these topologies, described in more detail in Section 3, are well-suited for characterizing various properties in the topological setting, they often forget geometric features determined by a choice of metric.
$\pi _{n}^{\text{sh}}(X,x_0)$
the structure of a pro-discrete group and is closely related to Dugundji’s pre-shape-theory approach in [Reference Dugundji16]. While these topologies, described in more detail in Section 3, are well-suited for characterizing various properties in the topological setting, they often forget geometric features determined by a choice of metric.
In this paper, we show that a metric space
![]() $(X,d)$
with basepoint
$(X,d)$
with basepoint
![]() $x_0\in X$
determines a pseudometric
$x_0\in X$
determines a pseudometric
![]() $\rho$
on
$\rho$
on
![]() $\pi _n(X,x_0)$
. While the vast majority of papers on topologized homotopy groups focus on the fundamental group, our results hold in arbitrary dimensions. The resulting pseudometric group
$\pi _n(X,x_0)$
. While the vast majority of papers on topologized homotopy groups focus on the fundamental group, our results hold in arbitrary dimensions. The resulting pseudometric group
![]() $(\pi _n(X,x_0),\rho )$
gives the
$(\pi _n(X,x_0),\rho )$
gives the
![]() $n$
-th homotopy group the structure of a topological group (Proposition 4.6), which we denote as
$n$
-th homotopy group the structure of a topological group (Proposition 4.6), which we denote as
![]() $\pi _{n}^{\text{met}}(X,x_0)$
. For general metric spaces,
$\pi _{n}^{\text{met}}(X,x_0)$
. For general metric spaces,
![]() $\rho$
depends entirely on the given metric
$\rho$
depends entirely on the given metric
![]() $d$
and the topology on
$d$
and the topology on
![]() $\pi _{n}^{\text{met}}(X,x_0)$
induced by
$\pi _{n}^{\text{met}}(X,x_0)$
induced by
![]() $\rho$
may also vary (see Example 4.9). However, we show that when
$\rho$
may also vary (see Example 4.9). However, we show that when
![]() $X$
is compact, the topology of
$X$
is compact, the topology of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
induced by
$\pi _{n}^{\text{met}}(X,x_0)$
induced by
![]() $\rho$
is independent of the choice of metric
$\rho$
is independent of the choice of metric
![]() $d$
(Theorem 4.10). We prove these results in Section 4 after establishing the basic theory of
$d$
(Theorem 4.10). We prove these results in Section 4 after establishing the basic theory of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
$\pi _{n}^{\text{met}}(X,x_0)$
In Section 5, we prove the following theorem, which compares the topology of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
with the shape topology. Recall that a space
$\pi _{n}^{\text{met}}(X,x_0)$
with the shape topology. Recall that a space
![]() $X$
is
$X$
is
![]() $LC^{n}$
if for every open neighborhood
$LC^{n}$
if for every open neighborhood
![]() $U$
of a point
$U$
of a point
![]() $x\in X$
, there is an open neighborhood
$x\in X$
, there is an open neighborhood
![]() $V$
of
$V$
of
![]() $x$
such that
$x$
such that
![]() $V\subseteq U$
and such that every map
$V\subseteq U$
and such that every map
![]() $f\;:\;S^{k}\to V$
where
$f\;:\;S^{k}\to V$
where
![]() $0\leq k\leq n$
is null-homotopic in
$0\leq k\leq n$
is null-homotopic in
![]() $U$
. For all
$U$
. For all
![]() $n\geq 0$
, there are compact metric spaces which are
$n\geq 0$
, there are compact metric spaces which are
![]() $LC^n$
but not locally
$LC^n$
but not locally
![]() $n$
-connected.
$n$
-connected.
Theorem 1.1.
Let
![]() $(X,d)$
be a path-connected compact metric space and
$(X,d)$
be a path-connected compact metric space and
![]() $n\geq 1$
. The topology induced by the natural pseudometric
$n\geq 1$
. The topology induced by the natural pseudometric
![]() $\rho$
on
$\rho$
on
![]() $\pi _n(X,x_0)$
is at least as fine as the shape topology. Moreover, these two topologies agree in the following two cases:
$\pi _n(X,x_0)$
is at least as fine as the shape topology. Moreover, these two topologies agree in the following two cases:
-
1. if
 $X$
is
$X$
is
 $LC^{n-1}$
,
$LC^{n-1}$
, -
2. if
 $X=\varprojlim _{j\in \mathbb{N}}(X_j,r_{j+1,j})$
is an inverse limit of finite polyhedra where the bonding maps
$X=\varprojlim _{j\in \mathbb{N}}(X_j,r_{j+1,j})$
is an inverse limit of finite polyhedra where the bonding maps
 $r_{j+1,j}\;:\;X_{j+1}\to X_j$
are retractions.
$r_{j+1,j}\;:\;X_{j+1}\to X_j$
are retractions.
To prove this result, we show that for a compact metric space
![]() $(X,d)$
the pseudometric topology on
$(X,d)$
the pseudometric topology on
![]() $\pi _n(X,x_0)$
lies between the shape topology and a third topology called the Spanier topology (Definition 5.5). For Case (1), we apply a result from [Reference Aceti and Brazas3] to conclude that, in the
$\pi _n(X,x_0)$
lies between the shape topology and a third topology called the Spanier topology (Definition 5.5). For Case (1), we apply a result from [Reference Aceti and Brazas3] to conclude that, in the
![]() $LC^{n-1}$
case, the Spanier and shape topologies (and thus all three topologies) agree. We prove Case (2) separately using the fact that we may alter the metric on
$LC^{n-1}$
case, the Spanier and shape topologies (and thus all three topologies) agree. We prove Case (2) separately using the fact that we may alter the metric on
![]() $X$
without affecting the topologies of
$X$
without affecting the topologies of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
or
$\pi _{n}^{\text{met}}(X,x_0)$
or
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
.
$\pi _{n}^{\text{sh}}(X,x_0)$
.
While Case (2) may appear structurally restrictive, it provides insight to some prominent examples. For example, if
![]() $X$
is an infinite shrinking wedge of finite polyhedra
$X$
is an infinite shrinking wedge of finite polyhedra
![]() $X_j$
, then
$X_j$
, then
![]() $X$
may be identified with
$X$
may be identified with
![]() $\varprojlim _{k\in \mathbb{N}}\bigvee _{j=1}^{k}X_j$
, which has retraction bonding maps (see Example 5.17). While the higher homotopy groups of spaces of the form
$\varprojlim _{k\in \mathbb{N}}\bigvee _{j=1}^{k}X_j$
, which has retraction bonding maps (see Example 5.17). While the higher homotopy groups of spaces of the form
![]() $X$
are only known in some special cases [Reference Eda and Kawamura17], Theorem 5.18 implies that
$X$
are only known in some special cases [Reference Eda and Kawamura17], Theorem 5.18 implies that
![]() $\pi _{n}^{\text{met}}(X,x_0)\cong \pi _{n}^{\text{sh}}(X,x_0)$
for all
$\pi _{n}^{\text{met}}(X,x_0)\cong \pi _{n}^{\text{sh}}(X,x_0)$
for all
![]() $n\geq 1$
.
$n\geq 1$
.
The upshot of Case (1) of Theorem 1.1 is that in the presence of local
![]() $(n-1)$
-connectedness conditions, one can often characterize the pseudometric topology by appealing to shape-theoretic methods, which are likely to be simpler than an analysis of the uniform metric on the
$(n-1)$
-connectedness conditions, one can often characterize the pseudometric topology by appealing to shape-theoretic methods, which are likely to be simpler than an analysis of the uniform metric on the
![]() $n$
-th loop space. We can modify an example from [Reference Conner, Meilstrup, Repovs, Zastrow and Zeljko15] to show Theorem 1.1 does not hold for
$n$
-th loop space. We can modify an example from [Reference Conner, Meilstrup, Repovs, Zastrow and Zeljko15] to show Theorem 1.1 does not hold for
![]() $n\geq 1$
without the
$n\geq 1$
without the
![]() $LC^{0}$
condition (see Example 5.16). The authors do not know of a higher dimensional counterexample, that is, a Peano continuum
$LC^{0}$
condition (see Example 5.16). The authors do not know of a higher dimensional counterexample, that is, a Peano continuum
![]() $X$
and
$X$
and
![]() $n\geq 2$
for which the pseudometric topology on
$n\geq 2$
for which the pseudometric topology on
![]() $\pi _n(X,x_0)$
is strictly finer than the shape topology. According to Theorem 1.1, such an example must fail to be
$\pi _n(X,x_0)$
is strictly finer than the shape topology. According to Theorem 1.1, such an example must fail to be
![]() $LC^{n-1}$
and also cannot be an inverse limit of retracts of finite polyhedra. This leaves the following problem.
$LC^{n-1}$
and also cannot be an inverse limit of retracts of finite polyhedra. This leaves the following problem.
Problem 1.2.
For
![]() $n\geq 2$
, give an example of a based Peano continuum
$n\geq 2$
, give an example of a based Peano continuum
![]() $(X,x_0)$
for which the topology of
$(X,x_0)$
for which the topology of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is strictly finer than that of
$\pi _{n}^{\text{met}}(X,x_0)$
is strictly finer than that of
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
.
$\pi _{n}^{\text{sh}}(X,x_0)$
.
2. Preliminaries
Throughout this paper,
![]() $(X,d)$
will denote a path-connected metric space with basepoint
$(X,d)$
will denote a path-connected metric space with basepoint
![]() $x_0\in X$
. The unit interval is denoted
$x_0\in X$
. The unit interval is denoted
![]() $[0,1]$
, the unit
$[0,1]$
, the unit
![]() $n$
-disk is denoted
$n$
-disk is denoted
![]() $D^n=\{\mathbf{x}\in \mathbb{R}^n\mid \|\mathbf{x}\|\leq 1\}$
, and
$D^n=\{\mathbf{x}\in \mathbb{R}^n\mid \|\mathbf{x}\|\leq 1\}$
, and
![]() $S^{n-1}=\partial D^n$
is the unit
$S^{n-1}=\partial D^n$
is the unit
![]() $(n-1)$
-sphere. The latter two spaces have basepoint
$(n-1)$
-sphere. The latter two spaces have basepoint
![]() $d_0=(1,0,\dots,0)$
. The
$d_0=(1,0,\dots,0)$
. The
![]() $n$
-th homotopy group of
$n$
-th homotopy group of
![]() $(X,x_0)$
is denoted
$(X,x_0)$
is denoted
![]() $\pi _n(X,x_0)$
. If
$\pi _n(X,x_0)$
. If
![]() $f\;:\;(X,x_0)\to (Y,y_0)$
is a based map, then
$f\;:\;(X,x_0)\to (Y,y_0)$
is a based map, then
![]() $f_{\#}\;:\;\pi _n(X,x_0)\to \pi _n(Y,y_0)$
is the induced homomorphism.
$f_{\#}\;:\;\pi _n(X,x_0)\to \pi _n(Y,y_0)$
is the induced homomorphism.
Let
![]() $\Omega ^n(X,x_0)$
be the space of maps
$\Omega ^n(X,x_0)$
be the space of maps
![]() $\alpha \;:\;([0,1]^n,\partial [0,1]^n)\to (X,x_0)$
based at
$\alpha \;:\;([0,1]^n,\partial [0,1]^n)\to (X,x_0)$
based at
![]() $x_0$
(which we call
$x_0$
(which we call
![]() $n$
-loops) with the metric of uniform convergence. It is well-known that the uniform metric topology agrees with the usual compact-open topology on
$n$
-loops) with the metric of uniform convergence. It is well-known that the uniform metric topology agrees with the usual compact-open topology on
![]() $\Omega ^{n}(X,x_0)$
(when convenient, we may identify
$\Omega ^{n}(X,x_0)$
(when convenient, we may identify
![]() $\Omega ^n(X,x_0)$
with the space of based maps
$\Omega ^n(X,x_0)$
with the space of based maps
![]() $(S^n,d_0)\to (X,x_0)$
also with the uniform metric). Let
$(S^n,d_0)\to (X,x_0)$
also with the uniform metric). Let
![]() $\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _n(X,x_0)$
,
$\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _n(X,x_0)$
,
![]() $\pi (\alpha )=[\alpha ]$
denote the canonical surjection taking a map
$\pi (\alpha )=[\alpha ]$
denote the canonical surjection taking a map
![]() $\alpha$
to its homotopy class.
$\alpha$
to its homotopy class.
Given
![]() $\alpha \in \Omega ^n(X,x_0)$
, let
$\alpha \in \Omega ^n(X,x_0)$
, let
![]() $\alpha ^{-}(t_1,t_2,\dots,t_n)=\alpha (1-t_1,t_2,\dots,t_n)$
denote the reverse of
$\alpha ^{-}(t_1,t_2,\dots,t_n)=\alpha (1-t_1,t_2,\dots,t_n)$
denote the reverse of
![]() $\alpha$
, and if
$\alpha$
, and if
![]() $\alpha _1,\alpha _2,\dots,\alpha _n$
is a sequence of
$\alpha _1,\alpha _2,\dots,\alpha _n$
is a sequence of
![]() $n$
-loops, then
$n$
-loops, then
![]() $\alpha _1\cdot \alpha _2\cdots \alpha _n$
is the usual
$\alpha _1\cdot \alpha _2\cdots \alpha _n$
is the usual
![]() $n$
-fold concatenation defined as
$n$
-fold concatenation defined as
![]() $\alpha _i$
on
$\alpha _i$
on
![]() $\left [\frac{i-1}{n},\frac{i}{n}\right ]\times [0,1]^{n-1}$
. Generally,
$\left [\frac{i-1}{n},\frac{i}{n}\right ]\times [0,1]^{n-1}$
. Generally,
![]() $c_{x_0}\in \Omega ^n(X,x_0)$
will denote the constant map at
$c_{x_0}\in \Omega ^n(X,x_0)$
will denote the constant map at
![]() $x_0$
so that
$x_0$
so that
![]() $e=[c_{x_0}]$
serves as the identity element of
$e=[c_{x_0}]$
serves as the identity element of
![]() $\pi _n(X,x_0)$
.
$\pi _n(X,x_0)$
.
3. Topologies on homotopy groups
Here, we briefly recall some previously studied topologies on the homotopy groups.
3.1. The quotient topology
Let
![]() $\pi _{n}^{\text{qtop}}(X,x_0)$
denote the
$\pi _{n}^{\text{qtop}}(X,x_0)$
denote the
![]() $n$
-th homotopy group with the quotient topology with respect to the canonical map
$n$
-th homotopy group with the quotient topology with respect to the canonical map
![]() $\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _n(X,x_0)$
, that is, the finest topology on
$\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _n(X,x_0)$
, that is, the finest topology on
![]() $\pi _n(X,x_0)$
such that
$\pi _n(X,x_0)$
such that
![]() $\pi$
is continuous. In particular,
$\pi$
is continuous. In particular,
![]() $A\subseteq \pi _{n}^{\text{qtop}}(X,x_0)$
is open (closed) if and only if
$A\subseteq \pi _{n}^{\text{qtop}}(X,x_0)$
is open (closed) if and only if
![]() $\pi ^{-1}(A)$
is open (closed) in
$\pi ^{-1}(A)$
is open (closed) in
![]() $\Omega ^{n}(X,x_0)$
. It is known that this topology gives
$\Omega ^{n}(X,x_0)$
. It is known that this topology gives
![]() $\pi _n(X,x_0)$
the structure of a quasitopological group [Reference Arhangel’skii and Tkachenko5] (in the sense that inversion is continuous and multiplication is continuous in each variable) which can fail to be a topological group [Reference Brazas8, Reference Fabel19, Reference Fabel20] even when
$\pi _n(X,x_0)$
the structure of a quasitopological group [Reference Arhangel’skii and Tkachenko5] (in the sense that inversion is continuous and multiplication is continuous in each variable) which can fail to be a topological group [Reference Brazas8, Reference Fabel19, Reference Fabel20] even when
![]() $X$
is a compact metric space. For a general study of
$X$
is a compact metric space. For a general study of
![]() $\pi _1$
with the quotient topology, we refer the reader to [Reference Brazas and Fabel11]. It is known that if
$\pi _1$
with the quotient topology, we refer the reader to [Reference Brazas and Fabel11]. It is known that if
![]() $X$
is locally
$X$
is locally
![]() $(n-1)$
-connected and semilocally
$(n-1)$
-connected and semilocally
![]() $n$
-connected, then
$n$
-connected, then
![]() $\Omega ^n(X,x_0)$
is locally path-connected [Reference Wada24]. In such a situation,
$\Omega ^n(X,x_0)$
is locally path-connected [Reference Wada24]. In such a situation,
![]() $\pi _{n}^{\text{qtop}}(X,x_0)$
is guaranteed to be discrete (see also [Reference Calcut and McCarthy14] in dimension
$\pi _{n}^{\text{qtop}}(X,x_0)$
is guaranteed to be discrete (see also [Reference Calcut and McCarthy14] in dimension
![]() $n=1$
). In particular, if
$n=1$
). In particular, if
![]() $X$
is a polyhedron, manifold, or CW-complex, then
$X$
is a polyhedron, manifold, or CW-complex, then
![]() $\pi _{n}^{\text{qtop}}(X,x_0)$
is a discrete group for all
$\pi _{n}^{\text{qtop}}(X,x_0)$
is a discrete group for all
![]() $n\geq 1$
.
$n\geq 1$
.
3.2. The “tau topology”
In [Reference Brazas9], it was observed that for any quasitopological group
![]() $G$
, there is a finest group topology on the group
$G$
, there is a finest group topology on the group
![]() $G$
, which is coarser than that of
$G$
, which is coarser than that of
![]() $G$
. The resulting topological group is denoted
$G$
. The resulting topological group is denoted
![]() $\tau (G)$
. In other words, the category of topological groups is a reflective subcategory of the category of quasitopological groups, where
$\tau (G)$
. In other words, the category of topological groups is a reflective subcategory of the category of quasitopological groups, where
![]() $\tau$
is the reflection functor. In the case of homotopy groups, the
$\tau$
is the reflection functor. In the case of homotopy groups, the
![]() $\tau$
-reflection
$\tau$
-reflection
![]() $\pi _{n}^{\tau }(X,x_0)=\tau (\pi _{n}^{\text{qtop}}(X,x_0))$
is a topological group. The topology of
$\pi _{n}^{\tau }(X,x_0)=\tau (\pi _{n}^{\text{qtop}}(X,x_0))$
is a topological group. The topology of
![]() $\pi _{n}^{\tau }(X,x_0)$
is coarser than that of
$\pi _{n}^{\tau }(X,x_0)$
is coarser than that of
![]() $\pi _{n}^{\text{qtop}}(X,x_0)$
and agrees with that of
$\pi _{n}^{\text{qtop}}(X,x_0)$
and agrees with that of
![]() $\pi _{n}^{\text{qtop}}(X,x_0)$
if and only if
$\pi _{n}^{\text{qtop}}(X,x_0)$
if and only if
![]() $\pi _{n}^{\text{qtop}}(X,x_0)$
is a topological group. The
$\pi _{n}^{\text{qtop}}(X,x_0)$
is a topological group. The
![]() $\tau$
-topology is the finest group topology on
$\tau$
-topology is the finest group topology on
![]() $\pi _{n}(X,x_0)$
for which
$\pi _{n}(X,x_0)$
for which
![]() $\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _{n}(X,x_0)$
is continuous. In [Reference Virk and Zastrow23], an analogous construction is given for the “universal path space,” i.e. the set of path-homotopy classes of paths in
$\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _{n}(X,x_0)$
is continuous. In [Reference Virk and Zastrow23], an analogous construction is given for the “universal path space,” i.e. the set of path-homotopy classes of paths in
![]() $X$
starting at
$X$
starting at
![]() $x_0$
.
$x_0$
.
3.3. The shape topology
We give a few details regarding the construction of the
![]() $n$
-th shape homotopy group and refer the reader to [Reference Mardešić and Segal21] for a detailed treatment of shape theory. Let
$n$
-th shape homotopy group and refer the reader to [Reference Mardešić and Segal21] for a detailed treatment of shape theory. Let
![]() ${\text{cov}}(X)$
be the directed set of pairs
${\text{cov}}(X)$
be the directed set of pairs
![]() $(\mathscr{U},U_0)$
where
$(\mathscr{U},U_0)$
where
![]() $\mathscr{U}$
is a locally finite open cover of
$\mathscr{U}$
is a locally finite open cover of
![]() $X$
and
$X$
and
![]() $U_0$
is a distinguished element of
$U_0$
is a distinguished element of
![]() $\mathscr{U}$
containing
$\mathscr{U}$
containing
![]() $x_0$
. Here,
$x_0$
. Here,
![]() ${\text{cov}}(X)$
is directed by refinement. Given
${\text{cov}}(X)$
is directed by refinement. Given
![]() $(\mathscr{U},U_0)\in{\text{cov}}(X)$
, let
$(\mathscr{U},U_0)\in{\text{cov}}(X)$
, let
![]() $N(\mathscr{U})$
be the abstract simplicial complex which is the nerve of
$N(\mathscr{U})$
be the abstract simplicial complex which is the nerve of
![]() $\mathscr{U}$
. In particular,
$\mathscr{U}$
. In particular,
![]() $\mathscr{U}$
is the vertex set of
$\mathscr{U}$
is the vertex set of
![]() $U$
and the n vertices
$U$
and the n vertices
![]() $U_1,\dots,U_n$
span an n-simplex
$U_1,\dots,U_n$
span an n-simplex
![]() $\Leftrightarrow$
$\Leftrightarrow$
![]() $\bigcap _{i=1}^{n}U_i\neq \emptyset$
. The geometric realization
$\bigcap _{i=1}^{n}U_i\neq \emptyset$
. The geometric realization
![]() $|N(\mathscr{U})|$
is a polyhedron, and thus,
$|N(\mathscr{U})|$
is a polyhedron, and thus,
![]() $\pi _n(|N(\mathscr{U})|,U_0)$
may be regarded naturally as a discrete group, for example if it is given the quotient topology.
$\pi _n(|N(\mathscr{U})|,U_0)$
may be regarded naturally as a discrete group, for example if it is given the quotient topology.
Given a pair
![]() $(\mathscr{V},V_0)$
which refines
$(\mathscr{V},V_0)$
which refines
![]() $(\mathscr{U},U_0)$
, a simplicial map
$(\mathscr{U},U_0)$
, a simplicial map
![]() $p_{\mathscr{U}\mathscr{V}}\;:\;|N(\mathscr{V})|\to |N(\mathscr{U})|$
is constructed by sending a vertex
$p_{\mathscr{U}\mathscr{V}}\;:\;|N(\mathscr{V})|\to |N(\mathscr{U})|$
is constructed by sending a vertex
![]() $V\in \mathscr{V}$
to some
$V\in \mathscr{V}$
to some
![]() $U\in \mathscr{U}$
for which
$U\in \mathscr{U}$
for which
![]() $V\subseteq U$
(in particular,
$V\subseteq U$
(in particular,
![]() $V_0$
is mapped to
$V_0$
is mapped to
![]() $U_0$
) and extending linearly. The map
$U_0$
) and extending linearly. The map
![]() $p_{\mathscr{U}\mathscr{V}}$
is unique up to homotopy and thus induces a unique homomorphism
$p_{\mathscr{U}\mathscr{V}}$
is unique up to homotopy and thus induces a unique homomorphism
![]() $p_{\mathscr{U}\mathscr{V}\#}\;:\;\pi _n(|N(\mathscr{V})|,V_0)\to \pi _n(|N(\mathscr{U})|,U_0)$
. The inverse system
$p_{\mathscr{U}\mathscr{V}\#}\;:\;\pi _n(|N(\mathscr{V})|,V_0)\to \pi _n(|N(\mathscr{U})|,U_0)$
. The inverse system
of discrete groups is the
![]() $n$
th pro-homotopy group and the limit
$n$
th pro-homotopy group and the limit
![]() $\check{\pi }_n(X,x_0)$
(topologized with the usual inverse limit topology) is the n-th shape homotopy group.
$\check{\pi }_n(X,x_0)$
(topologized with the usual inverse limit topology) is the n-th shape homotopy group.
Given a partition of unity
![]() $\{\phi _{U}\}_{U\in \mathscr{U}}$
subordinated to
$\{\phi _{U}\}_{U\in \mathscr{U}}$
subordinated to
![]() $\mathscr{U}$
and such that
$\mathscr{U}$
and such that
![]() $\phi _{U_0}(x_0)=1$
, a map
$\phi _{U_0}(x_0)=1$
, a map
![]() $p_{\mathscr{U}}\;:\;X\to |N(\mathscr{U})|$
is constructed by taking
$p_{\mathscr{U}}\;:\;X\to |N(\mathscr{U})|$
is constructed by taking
![]() $\phi _{U}(x)$
(for
$\phi _{U}(x)$
(for
![]() $x\in U$
,
$x\in U$
,
![]() $U\in \mathscr{U}$
) to be the barycentric coordinate of
$U\in \mathscr{U}$
) to be the barycentric coordinate of
![]() $p_{\mathscr{U}}(x)$
corresponding to the vertex
$p_{\mathscr{U}}(x)$
corresponding to the vertex
![]() $U$
. The induced continuous homomorphism
$U$
. The induced continuous homomorphism
![]() $p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _{n}(|N(\mathscr{U})|,U_0)$
satisfies
$p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _{n}(|N(\mathscr{U})|,U_0)$
satisfies
![]() $p_{\mathscr{U}\#}\circ p_{\mathscr{U}\mathscr{V}\#}=p_{\mathscr{V}\#}$
whenever
$p_{\mathscr{U}\#}\circ p_{\mathscr{U}\mathscr{V}\#}=p_{\mathscr{V}\#}$
whenever
![]() $(\mathscr{V},V_0)$
refines
$(\mathscr{V},V_0)$
refines
![]() $(\mathscr{U},U_0)$
. Thus, there is a canonical, continuous homomorphism
$(\mathscr{U},U_0)$
. Thus, there is a canonical, continuous homomorphism
![]() $\Psi _n\;:\;\pi _n(X,x_0)\to \check{\pi }_{n}(X,x_0)$
to the
$\Psi _n\;:\;\pi _n(X,x_0)\to \check{\pi }_{n}(X,x_0)$
to the
![]() $n$
-th shape homotopy group, given by
$n$
-th shape homotopy group, given by
![]() $\Psi _n([\alpha ])=([p_{\mathscr{U}}\circ \alpha ])_{\mathscr{U}}$
.
$\Psi _n([\alpha ])=([p_{\mathscr{U}}\circ \alpha ])_{\mathscr{U}}$
.
Definition 3.1.
The shape topology on
![]() $\pi _n(X,x_0)$
is the initial topology with respect to the
$\pi _n(X,x_0)$
is the initial topology with respect to the
![]() $n$
-th shape homomorphism
$n$
-th shape homomorphism
![]() $\Psi _n\;:\;\pi _n(X,x_0)\to \check{\pi }_{n}(X,x_0)$
described above. Let
$\Psi _n\;:\;\pi _n(X,x_0)\to \check{\pi }_{n}(X,x_0)$
described above. Let
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
denote
$\pi _{n}^{\text{sh}}(X,x_0)$
denote
![]() $\pi _n(X,x_0)$
equipped with the shape topology.
$\pi _n(X,x_0)$
equipped with the shape topology.
The shape topology is characterized as follows:
![]() $A\subset \pi _{n}^{\text{sh}}(X,x_0)$
is open (resp. closed)
$A\subset \pi _{n}^{\text{sh}}(X,x_0)$
is open (resp. closed)
![]() $\Leftrightarrow$
$\Leftrightarrow$
![]() $A=\Psi _{n}^{-1}(B)$
for an open (resp. closed) set
$A=\Psi _{n}^{-1}(B)$
for an open (resp. closed) set
![]() $B\subset \check{\pi }_{n}(X,x_0)$
. Equivalently, a neighborhood base at the identity element is formed by the normal subgroups
$B\subset \check{\pi }_{n}(X,x_0)$
. Equivalently, a neighborhood base at the identity element is formed by the normal subgroups
![]() $\ker (p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _n(|N(\mathscr{U})|,U_0))$
,
$\ker (p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _n(|N(\mathscr{U})|,U_0))$
,
![]() $(\mathscr{U},U_0)\in{\text{cov}}(X)$
. Since
$(\mathscr{U},U_0)\in{\text{cov}}(X)$
. Since
![]() $\check{\pi }_{n}(X,x_0)$
is a topological group, it follows immediately that
$\check{\pi }_{n}(X,x_0)$
is a topological group, it follows immediately that
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
is a topological group.
$\pi _{n}^{\text{sh}}(X,x_0)$
is a topological group.
Proposition 3.2 ([Reference Brazas9], 3.24). For any space
![]() $X$
, the shape topology of
$X$
, the shape topology of
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
is coarser than that of
$\pi _{n}^{\text{sh}}(X,x_0)$
is coarser than that of
![]() $\pi _{n}^{\tau }(X,x_0)$
.
$\pi _{n}^{\tau }(X,x_0)$
.
Definition 3.3.
We say a space
![]() $X$
is
$X$
is
![]() $\pi _n$
-shape injective if
$\pi _n$
-shape injective if
![]() $\Psi _n:\pi _{n}(X,x_0)\to \check{\pi }_{n}(X,x_0)$
is a monomorphism.
$\Psi _n:\pi _{n}(X,x_0)\to \check{\pi }_{n}(X,x_0)$
is a monomorphism.
By construction,
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
is Hausdorff
$\pi _{n}^{\text{sh}}(X,x_0)$
is Hausdorff
![]() $\Leftrightarrow$
$\Leftrightarrow$
![]() $X$
is
$X$
is
![]() $\pi _n$
-shape injective.
$\pi _n$
-shape injective.
4. A pseudometric on homotopy groups
Let
![]() $(X,d)$
be a path-connected metric space and consider the uniform metric
$(X,d)$
be a path-connected metric space and consider the uniform metric
on
![]() $\Omega ^n(X,x_0)$
. Observe that
$\Omega ^n(X,x_0)$
. Observe that
and
![]() $\mu (\alpha,\beta )=\mu (\alpha ^{-},\beta ^{-})$
. We consider the following function
$\mu (\alpha,\beta )=\mu (\alpha ^{-},\beta ^{-})$
. We consider the following function
![]() $\rho \;:\;\pi _{n}(X,x_0)\times \pi _{n}(X,x_0)\to [0,\infty )$
on the homotopy group
$\rho \;:\;\pi _{n}(X,x_0)\times \pi _{n}(X,x_0)\to [0,\infty )$
on the homotopy group
![]() $\pi _{n}(X,x_0)$
:
$\pi _{n}(X,x_0)$
:
We will show below that
![]() $\rho$
is a pseudometric on
$\rho$
is a pseudometric on
![]() $\pi _{n}(X,x_0)$
. Certainly,
$\pi _{n}(X,x_0)$
. Certainly,
![]() $\rho$
is symmetric and
$\rho$
is symmetric and
![]() $\rho (a,a)=0$
; however, a little more work is required to verify the triangle inequality.
$\rho (a,a)=0$
; however, a little more work is required to verify the triangle inequality.
Remark 4.1.
In general, if
![]() $(X,d)$
is a metric space,
$(X,d)$
is a metric space,
![]() $\sim$
is an equivalence relation, and
$\sim$
is an equivalence relation, and
![]() $Y=X/\mathord{\sim }$
, then the definition
$Y=X/\mathord{\sim }$
, then the definition
![]() $\rho \;:\; Y\times Y\to [0,\infty )$
,
$\rho \;:\; Y\times Y\to [0,\infty )$
,
![]() $\rho (a,b)=\inf \{d(\alpha,\beta )\mid \alpha \in a,\beta \in b\}$
need not satisfy the triangle inequality. In our situation, we must make use of the group structure of
$\rho (a,b)=\inf \{d(\alpha,\beta )\mid \alpha \in a,\beta \in b\}$
need not satisfy the triangle inequality. In our situation, we must make use of the group structure of
![]() $\pi _{n}(X,x_0)$
and the nature of the uniform metric
$\pi _{n}(X,x_0)$
and the nature of the uniform metric
![]() $\mu$
in order to verify the triangle inequality.
$\mu$
in order to verify the triangle inequality.
In the next three results, we assume
![]() $(X,d)$
is an arbitrary metric space,
$(X,d)$
is an arbitrary metric space,
![]() $x_0\in X$
, and
$x_0\in X$
, and
![]() $\mu$
and
$\mu$
and
![]() $\rho$
are defined as above.
$\rho$
are defined as above.
Lemma 4.2 (Isometric Inversion). For all
![]() $a,b\in \pi _{n}(X,x_0)$
, we have
$a,b\in \pi _{n}(X,x_0)$
, we have
![]() $\rho (a,b)=\rho (a^{-1},b^{-1})$
.
$\rho (a,b)=\rho (a^{-1},b^{-1})$
.
Proof. Since
![]() $\mu (\alpha,\beta )=\mu (\alpha ^{-},\beta ^{-})$
for all
$\mu (\alpha,\beta )=\mu (\alpha ^{-},\beta ^{-})$
for all
![]() $\alpha \in a$
,
$\alpha \in a$
,
![]() $\beta \in b$
, it is clear that
$\beta \in b$
, it is clear that
Lemma 4.3 (Isometric translations). For all
![]() $a,b,c\in \pi _{n}(X,x_0)$
, we have
$a,b,c\in \pi _{n}(X,x_0)$
, we have
![]() $\rho (a,b)=\rho (ac,bc)=\rho (ca,cb)$
.
$\rho (a,b)=\rho (ac,bc)=\rho (ca,cb)$
.
Proof. Fix
![]() $a,b,c\in \pi _{n}(X,x_0)$
and
$a,b,c\in \pi _{n}(X,x_0)$
and
![]() $\alpha \in a$
,
$\alpha \in a$
,
![]() $\beta \in b$
, and
$\beta \in b$
, and
![]() $\gamma \in c$
. We have
$\gamma \in c$
. We have
![]() $\mu (\alpha \cdot \gamma,\beta \cdot \gamma )=\mu (\alpha,\beta )$
. It follows that
$\mu (\alpha \cdot \gamma,\beta \cdot \gamma )=\mu (\alpha,\beta )$
. It follows that
The symmetric argument gives
![]() $\rho (a,b)=\rho (ca,cb)$
.
$\rho (a,b)=\rho (ca,cb)$
.
Lemma 4.4.
For all
![]() $a,b\in \pi _{n}(X,x_0)$
, we have
$a,b\in \pi _{n}(X,x_0)$
, we have
![]() $\rho (ab,e)\leq \max \{\rho (a,e),\rho (b,e)\}$
$\rho (ab,e)\leq \max \{\rho (a,e),\rho (b,e)\}$
Proof. Suppose
![]() $a,b\in \pi _{n}(X,x_0)$
and
$a,b\in \pi _{n}(X,x_0)$
and
![]() $\epsilon \gt 0$
. Find
$\epsilon \gt 0$
. Find
![]() $\alpha \in a$
,
$\alpha \in a$
,
![]() $\beta \in b$
, and
$\beta \in b$
, and
![]() $\gamma _1,\gamma _2\in e=[c_{x_0}]$
such that
$\gamma _1,\gamma _2\in e=[c_{x_0}]$
such that
![]() $\mu (\alpha,\gamma _1)\lt \rho (a,e)+\dfrac{\epsilon }{2}$
and
$\mu (\alpha,\gamma _1)\lt \rho (a,e)+\dfrac{\epsilon }{2}$
and
![]() $\mu (\beta,\gamma _2)\lt \rho (b,e)+\dfrac{\epsilon }{2}$
. Note that
$\mu (\beta,\gamma _2)\lt \rho (b,e)+\dfrac{\epsilon }{2}$
. Note that
 \begin{align*} \mu (\alpha \cdot \beta,\gamma _1\cdot \gamma _2) & = \max \{\mu (\alpha,\gamma _1),\mu (\beta,\gamma _2)\}\nonumber\\ &\lt \max \left \{\rho (a,e)+\frac{\epsilon }{2},\rho (b,e)+\frac{\epsilon }{2}\right \}\\ &\lt \max \left \{\rho (a,e),\rho (b,e)\right \}+\epsilon\nonumber \end{align*}
\begin{align*} \mu (\alpha \cdot \beta,\gamma _1\cdot \gamma _2) & = \max \{\mu (\alpha,\gamma _1),\mu (\beta,\gamma _2)\}\nonumber\\ &\lt \max \left \{\rho (a,e)+\frac{\epsilon }{2},\rho (b,e)+\frac{\epsilon }{2}\right \}\\ &\lt \max \left \{\rho (a,e),\rho (b,e)\right \}+\epsilon\nonumber \end{align*}
Thus,
![]() $\rho (ab,e)\leq \max \left \{\rho (a,e),\rho (b,e)\right \}$
.
$\rho (ab,e)\leq \max \left \{\rho (a,e),\rho (b,e)\right \}$
.
Theorem 4.5.
For any metric space
![]() $(X,d)$
, the function
$(X,d)$
, the function
![]() $\rho \;:\;\pi _{n}(X,x_0)\times \pi _{n}(X,x_0)\to [0,\infty )$
, defined above, is a pseudometric on
$\rho \;:\;\pi _{n}(X,x_0)\times \pi _{n}(X,x_0)\to [0,\infty )$
, defined above, is a pseudometric on
![]() $\pi _{n}(X,x_0)$
.
$\pi _{n}(X,x_0)$
.
Proof. As noted above, it suffices to verify the triangle inequality. Let
![]() $a,b,c\in \pi _{n}(X,x_0)$
. Using the previous three lemmas, we have:
$a,b,c\in \pi _{n}(X,x_0)$
. Using the previous three lemmas, we have:
 \begin{align*} \rho (a,c) & = \rho (ac^{-1},e) \\ &= \rho (ab^{-1}bc,e) \\ &\leq \max \{\rho (ab^{-1},e),\rho (bc^{-1},e)\} \\ &= \max \{\rho (ab^{-1},e),\rho (cb^{-1},e)\} \\ &\leq \rho (ab^{-1},e)+\rho (cb^{-1},e)\\ &= \rho (a,b)+\rho (c,b) \\ &= \rho (a,b)+\rho (b,c) \end{align*}
\begin{align*} \rho (a,c) & = \rho (ac^{-1},e) \\ &= \rho (ab^{-1}bc,e) \\ &\leq \max \{\rho (ab^{-1},e),\rho (bc^{-1},e)\} \\ &= \max \{\rho (ab^{-1},e),\rho (cb^{-1},e)\} \\ &\leq \rho (ab^{-1},e)+\rho (cb^{-1},e)\\ &= \rho (a,b)+\rho (c,b) \\ &= \rho (a,b)+\rho (b,c) \end{align*}
Proposition 4.6.
Let
![]() $(X,d)$
be any metric space and
$(X,d)$
be any metric space and
![]() $x_0\in X$
. Equipped with the topology induced by the pseudometric
$x_0\in X$
. Equipped with the topology induced by the pseudometric
![]() $\rho$
,
$\rho$
,
![]() $\pi _{n}(X,x_0)$
is a topological group whose open balls
$\pi _{n}(X,x_0)$
is a topological group whose open balls
![]() $B_{\rho }(e,r)=\{a\in \pi _n(X,x_0)\mid \rho (e,a)\lt r\}$
,
$B_{\rho }(e,r)=\{a\in \pi _n(X,x_0)\mid \rho (e,a)\lt r\}$
,
![]() $r\gt 0$
are open normal subgroups.
$r\gt 0$
are open normal subgroups.
Proof. Since the open balls
![]() $B_{\rho }(e,r)$
form a neighborhood base at
$B_{\rho }(e,r)$
form a neighborhood base at
![]() $e$
and translations are homeomorphisms (Lemma 4.3), it will follow that
$e$
and translations are homeomorphisms (Lemma 4.3), it will follow that
![]() $\pi _{n}(X,x_0)$
is a topological group once we show that
$\pi _{n}(X,x_0)$
is a topological group once we show that
![]() $B_{\rho }(e,r)$
is an open normal subgroup.
$B_{\rho }(e,r)$
is an open normal subgroup.
Since
![]() $\rho (a,e)=\rho (a^{-1},e)$
,
$\rho (a,e)=\rho (a^{-1},e)$
,
![]() $B_{\rho }(e,r)$
is closed under inversion. Additionally, by Lemma 4.3, we have
$B_{\rho }(e,r)$
is closed under inversion. Additionally, by Lemma 4.3, we have
for all
![]() $a,b\in \pi _{n}(X,x_0)$
. Thus,
$a,b\in \pi _{n}(X,x_0)$
. Thus,
![]() $B_{\rho }(e,r)$
is closed under conjugation (particularly when
$B_{\rho }(e,r)$
is closed under conjugation (particularly when
![]() $n=1$
). Finally, if
$n=1$
). Finally, if
![]() $\rho (a,e))\lt r$
and
$\rho (a,e))\lt r$
and
![]() $\rho (b,e)\lt r$
, then
$\rho (b,e)\lt r$
, then
![]() $\rho (ab,e)\leq \max \left \{\rho (a,e),\rho (b,e)\right \}\lt r$
by Lemma 4.4 and it follows that
$\rho (ab,e)\leq \max \left \{\rho (a,e),\rho (b,e)\right \}\lt r$
by Lemma 4.4 and it follows that
![]() $B_{\rho }(e,r)$
is closed under multiplication.
$B_{\rho }(e,r)$
is closed under multiplication.
Definition 4.7.
For a metric space
![]() $(X,d)$
and
$(X,d)$
and
![]() $x_0\in X$
, let
$x_0\in X$
, let
![]() $\pi _{n}^{\text{met}}(X,x_0)$
denote the
$\pi _{n}^{\text{met}}(X,x_0)$
denote the
![]() $n$
-th homotopy group equipped with the topology induced by the pseudometric
$n$
-th homotopy group equipped with the topology induced by the pseudometric
![]() $\rho$
. We call this topology the pseudometric topology (induced by
$\rho$
. We call this topology the pseudometric topology (induced by
![]() $d$
).
$d$
).
Since
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is a topological group, open subgroups of
$\pi _{n}^{\text{met}}(X,x_0)$
is a topological group, open subgroups of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
are also closed. Therefore,
$\pi _{n}^{\text{met}}(X,x_0)$
are also closed. Therefore,
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is zero-dimensional. On the other hand,
$\pi _{n}^{\text{met}}(X,x_0)$
is zero-dimensional. On the other hand,
![]() $\pi _{n}^{\text{met}}(X,x_0)$
need not be Hausdorff, since the closed normal subgroup
$\pi _{n}^{\text{met}}(X,x_0)$
need not be Hausdorff, since the closed normal subgroup
![]() $\bigcap _{r\gt 0}B_{\rho }(e,r)=\{a\in \pi _n(X,x_0)\mid \rho (a,e)=0\}$
is equal to
$\bigcap _{r\gt 0}B_{\rho }(e,r)=\{a\in \pi _n(X,x_0)\mid \rho (a,e)=0\}$
is equal to
![]() $\overline{\{e\}}$
, the closure of the identity element, which may be non-trivial. In particular,
$\overline{\{e\}}$
, the closure of the identity element, which may be non-trivial. In particular,
![]() $\overline{\{e\}}$
is non-trivial if and only if there exist sequences
$\overline{\{e\}}$
is non-trivial if and only if there exist sequences
![]() $\{\alpha _k\}_{k\in \mathbb{N}}$
and
$\{\alpha _k\}_{k\in \mathbb{N}}$
and
![]() $\{\beta _k\}_{k\in \mathbb{N}}$
in
$\{\beta _k\}_{k\in \mathbb{N}}$
in
![]() $\Omega ^{n}(X,x_0)$
such that
$\Omega ^{n}(X,x_0)$
such that
![]() $[\alpha _k]=[\alpha _{k+1}]$
,
$[\alpha _k]=[\alpha _{k+1}]$
,
![]() $[\beta _k]=[\beta _{k+1}]$
and
$[\beta _k]=[\beta _{k+1}]$
and
![]() $\displaystyle \lim _{k\to \infty }\mu (\alpha _k,\beta _k)=0$
.
$\displaystyle \lim _{k\to \infty }\mu (\alpha _k,\beta _k)=0$
.
Proposition 4.8.
Let
![]() $(X,d)$
and
$(X,d)$
and
![]() $(Y,d^{\prime})$
be metric spaces respectively inducing psuedometric
$(Y,d^{\prime})$
be metric spaces respectively inducing psuedometric
![]() $\rho$
on
$\rho$
on
![]() $\pi _n(X,x_0)$
and
$\pi _n(X,x_0)$
and
![]() $\rho^{\prime}$
on
$\rho^{\prime}$
on
![]() $\pi _n(Y,y_0)$
. If
$\pi _n(Y,y_0)$
. If
![]() $f\;:\;(X,d)\to (Y,d^{\prime})$
is a uniformly continuous map such that
$f\;:\;(X,d)\to (Y,d^{\prime})$
is a uniformly continuous map such that
![]() $f(x_0)=y_0$
, then the induced homomorphism
$f(x_0)=y_0$
, then the induced homomorphism
![]() $f_{\#}\;:\;(\pi _{n}^{\text{met}}(X,x_0),\rho )\to (\pi _{n}^{\text{met}}(Y,y_0),\rho^{\prime})$
is uniformly continuous.
$f_{\#}\;:\;(\pi _{n}^{\text{met}}(X,x_0),\rho )\to (\pi _{n}^{\text{met}}(Y,y_0),\rho^{\prime})$
is uniformly continuous.
Proof. Let
![]() $\mu$
and
$\mu$
and
![]() $\mu^{\prime}$
be the uniform metrics on
$\mu^{\prime}$
be the uniform metrics on
![]() $\Omega ^n(X,x_0)$
and
$\Omega ^n(X,x_0)$
and
![]() $\Omega ^n(Y,y_0)$
, respectively. Suppose
$\Omega ^n(Y,y_0)$
, respectively. Suppose
![]() $\epsilon \gt 0$
. There is a
$\epsilon \gt 0$
. There is a
![]() $\delta \gt 0$
such that
$\delta \gt 0$
such that
![]() $\mu (\alpha,\beta )\lt \delta$
$\mu (\alpha,\beta )\lt \delta$
![]() $\Rightarrow$
$\Rightarrow$
![]() $\mu^{\prime}(f\circ \alpha,f\circ \beta )\lt \epsilon/2$
. Suppose
$\mu^{\prime}(f\circ \alpha,f\circ \beta )\lt \epsilon/2$
. Suppose
![]() $\rho (g,h)\lt \delta$
for
$\rho (g,h)\lt \delta$
for
![]() $g,h\in \pi _{n}^{\text{met}}(X,x_0)$
. There are
$g,h\in \pi _{n}^{\text{met}}(X,x_0)$
. There are
![]() $\alpha \in g$
,
$\alpha \in g$
,
![]() $\beta \in h$
such that
$\beta \in h$
such that
![]() $\mu (\alpha,\beta )\lt \delta$
. Thus,
$\mu (\alpha,\beta )\lt \delta$
. Thus,
![]() $\mu^{\prime}(f\circ \alpha,f\circ \beta )\lt \epsilon/2$
. It follows that
$\mu^{\prime}(f\circ \alpha,f\circ \beta )\lt \epsilon/2$
. It follows that
![]() $\rho^{\prime}(f_{\#}(g),f_{\#}(h))=\rho^{\prime}([f\circ \alpha ],[f\circ \beta ])\lt \epsilon$
.
$\rho^{\prime}(f_{\#}(g),f_{\#}(h))=\rho^{\prime}([f\circ \alpha ],[f\circ \beta ])\lt \epsilon$
.
The following example illustrates that, in general, the topology on
![]() $\pi _{n}^{\text{met}}(X,x_0)$
induced by the pseudometric
$\pi _{n}^{\text{met}}(X,x_0)$
induced by the pseudometric
![]() $\rho$
may vary with our original choice of metric on
$\rho$
may vary with our original choice of metric on
![]() $X$
.
$X$
.
Example 4.9.
The cylinder
![]() $X=\mathbb{R}\times S^n$
and punctured real space
$X=\mathbb{R}\times S^n$
and punctured real space
![]() $Y=\mathbb{R}^{n+1}\backslash \{\mathbf{0}\}$
(with the Euclidean metrics) are homeomorphic and may be identified as topological spaces. However, the resulting pseudometrics on the
$Y=\mathbb{R}^{n+1}\backslash \{\mathbf{0}\}$
(with the Euclidean metrics) are homeomorphic and may be identified as topological spaces. However, the resulting pseudometrics on the
![]() $n$
-th homotopy group induced non-equivalent group topologies. In particular, if
$n$
-th homotopy group induced non-equivalent group topologies. In particular, if
![]() $x_0=(0,d_0)$
, then the resulting pseudometric
$x_0=(0,d_0)$
, then the resulting pseudometric
![]() $\rho _1$
on
$\rho _1$
on
![]() $\pi _n(\mathbb{R}\times S^n,x_0)$
is discrete. For a proof, one could apply Lemma 5.1 below to see that
$\pi _n(\mathbb{R}\times S^n,x_0)$
is discrete. For a proof, one could apply Lemma 5.1 below to see that
![]() $\pi _{n}^{\text{met}}(S^n,d_0)$
is discrete and then apply Proposition 4.8 to the projection map
$\pi _{n}^{\text{met}}(S^n,d_0)$
is discrete and then apply Proposition 4.8 to the projection map
![]() $\mathbb{R}\times S^n\to S^n$
. On the other hand, let
$\mathbb{R}\times S^n\to S^n$
. On the other hand, let
![]() $\rho _2$
denote the resulting pseudometric on
$\rho _2$
denote the resulting pseudometric on
![]() $\pi _n(Y,d_0)$
. For
$\pi _n(Y,d_0)$
. For
![]() $n\geq 2$
, let
$n\geq 2$
, let
![]() $\gamma _n:[0,1]\to Y$
to be the linear path from
$\gamma _n:[0,1]\to Y$
to be the linear path from
![]() $d_0$
to
$d_0$
to
![]() $(1/n,0,\dots,0)$
and let
$(1/n,0,\dots,0)$
and let
![]() $\alpha _n:S^n\to Y$
be the embedding of the n-sphere of radius
$\alpha _n:S^n\to Y$
be the embedding of the n-sphere of radius
![]() $1/n$
centered at the origin. Now consider the path-conjugates
$1/n$
centered at the origin. Now consider the path-conjugates
![]() $\gamma _n\ast \alpha _n$
, all of which represent a generator
$\gamma _n\ast \alpha _n$
, all of which represent a generator
![]() $g$
of
$g$
of
![]() $\pi _n(Y,y_0)\cong \mathbb{Z}$
. The path-conjugate
$\pi _n(Y,y_0)\cong \mathbb{Z}$
. The path-conjugate
![]() $\gamma _n\ast c_{n}$
is null-homotopic (where
$\gamma _n\ast c_{n}$
is null-homotopic (where
![]() $c_n\in \Omega ^n(Y,\gamma _n(1))$
is the constant map) and
$c_n\in \Omega ^n(Y,\gamma _n(1))$
is the constant map) and
Thus,
![]() $\rho _2(g,1)=0$
. It follows that the resulting pseudometric group
$\rho _2(g,1)=0$
. It follows that the resulting pseudometric group
![]() $\pi _{n}^{\text{met}}(Y,d_0)$
is indiscrete.
$\pi _{n}^{\text{met}}(Y,d_0)$
is indiscrete.
Theorem 4.10.
If
![]() $X$
is a path-connected, compact, metrizable topological space, and
$X$
is a path-connected, compact, metrizable topological space, and
![]() $x_0\in X$
, then the homeomorphism type of
$x_0\in X$
, then the homeomorphism type of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is independent of the choice of metric on
$\pi _{n}^{\text{met}}(X,x_0)$
is independent of the choice of metric on
![]() $X$
.
$X$
.
Proof. Suppose metrics
![]() $d_1$
and
$d_1$
and
![]() $d_2$
both induced the topology of
$d_2$
both induced the topology of
![]() $X$
. Let
$X$
. Let
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
be the respective pseudometrics on
$\rho _2$
be the respective pseudometrics on
![]() $\pi _n(X,x_0)$
. Since
$\pi _n(X,x_0)$
. Since
![]() $X$
is compact, the identity maps
$X$
is compact, the identity maps
![]() $id:(X,d_1)\to (X,d_2)$
and
$id:(X,d_1)\to (X,d_2)$
and
![]() $id:(X,d_2)\to (X,d_1)$
are uniformly continuous. By Proposition 4.8, the induced identity homomorphisms
$id:(X,d_2)\to (X,d_1)$
are uniformly continuous. By Proposition 4.8, the induced identity homomorphisms
![]() $(\pi _n(X,x_0),\rho _1)\to (\pi _n(X,x_0),\rho _2)$
and
$(\pi _n(X,x_0),\rho _1)\to (\pi _n(X,x_0),\rho _2)$
and
![]() $(\pi _n(X,x_0),\rho _2)\to (\pi _n(X,x_0),\rho _1)$
(with the respective pseudometrics) are continuous and thus inverse isomorphisms.
$(\pi _n(X,x_0),\rho _2)\to (\pi _n(X,x_0),\rho _1)$
(with the respective pseudometrics) are continuous and thus inverse isomorphisms.
Next, we observe that, in general, the isomorphism class of the topological group
![]() $\pi _{n}^{\text{met}}(X,x_0)$
does not depend on the choice of basepoint. Fix a retraction
$\pi _{n}^{\text{met}}(X,x_0)$
does not depend on the choice of basepoint. Fix a retraction
![]() $r:S^n\times [0,1]\to S^n\times \{0\}\cup \{d_0\}\times [0,1]$
. For any path
$r:S^n\times [0,1]\to S^n\times \{0\}\cup \{d_0\}\times [0,1]$
. For any path
![]() $\gamma \;:\;[0,1]\to X$
and map
$\gamma \;:\;[0,1]\to X$
and map
![]() $\alpha \;:\;(S^n,d_0)\to (X,\gamma (1))$
, we define the path-conjugate
$\alpha \;:\;(S^n,d_0)\to (X,\gamma (1))$
, we define the path-conjugate
![]() $\gamma \ast \alpha \;:\;(S^n,d_0)\to (X,\gamma (0))$
to be the composition of
$\gamma \ast \alpha \;:\;(S^n,d_0)\to (X,\gamma (0))$
to be the composition of
![]() $r(d,0)\;:\;S^n\to S^n\times \{0\}\cup \{d_0\}\times [0,1]$
followed by applying
$r(d,0)\;:\;S^n\to S^n\times \{0\}\cup \{d_0\}\times [0,1]$
followed by applying
![]() $\gamma$
to
$\gamma$
to
![]() $\{d_0\}\times [0,1]$
and
$\{d_0\}\times [0,1]$
and
![]() $\alpha$
to
$\alpha$
to
![]() $ S^n\times \{0\}$
. This defines a natural map
$ S^n\times \{0\}$
. This defines a natural map
![]() $\Omega ^n(X,\gamma (1))\to \Omega ^n(X,\gamma (0))$
,
$\Omega ^n(X,\gamma (1))\to \Omega ^n(X,\gamma (0))$
,
![]() $\beta \mapsto \gamma \ast \beta$
, which induces a change-of-basepoint isomorphism
$\beta \mapsto \gamma \ast \beta$
, which induces a change-of-basepoint isomorphism
![]() $\Gamma \;:\;\pi _n(X,\gamma (1))\to \pi _n(X,\gamma (0))$
on homotopy classes. Moreover, when
$\Gamma \;:\;\pi _n(X,\gamma (1))\to \pi _n(X,\gamma (0))$
on homotopy classes. Moreover, when
![]() $\gamma$
is a loop, the action of loops on
$\gamma$
is a loop, the action of loops on
![]() $n$
-loops defines a jointly continuous map
$n$
-loops defines a jointly continuous map
![]() $\Omega (X,x_0)\times \Omega ^n(X,x_0)\to \Omega ^n(X,x_0)$
,
$\Omega (X,x_0)\times \Omega ^n(X,x_0)\to \Omega ^n(X,x_0)$
,
![]() $(\gamma,\alpha )\mapsto \gamma \ast \alpha$
. This map induces the usual
$(\gamma,\alpha )\mapsto \gamma \ast \alpha$
. This map induces the usual
![]() $\pi _1$
-action
$\pi _1$
-action
![]() $[\gamma ]\ast [\alpha ]=[\gamma \ast \alpha ]$
on
$[\gamma ]\ast [\alpha ]=[\gamma \ast \alpha ]$
on
![]() $\pi _n(X,x_0)$
.
$\pi _n(X,x_0)$
.
Proposition 4.11.
For any path
![]() $\gamma \;:\;[0,1]\to X$
, the group isomorphism
$\gamma \;:\;[0,1]\to X$
, the group isomorphism
![]() $\Gamma ([\beta ])=[\gamma \ast \beta ]$
is an isometry.
$\Gamma ([\beta ])=[\gamma \ast \beta ]$
is an isometry.
Proof. For all
![]() $\alpha,\beta \in \Omega ^n(X,\gamma (1))$
, we have
$\alpha,\beta \in \Omega ^n(X,\gamma (1))$
, we have
![]() $\mu (\alpha,\beta )=\mu (\gamma \ast \alpha,\gamma \ast \beta )$
and thus
$\mu (\alpha,\beta )=\mu (\gamma \ast \alpha,\gamma \ast \beta )$
and thus
Thus
![]() $\Gamma$
is non-expansive. The inverse
$\Gamma$
is non-expansive. The inverse
![]() $\Gamma ^{-1}\;:\;\pi _{1}^{\text{met}}(X,\gamma (0))\to \pi _{1}^{\text{met}}(X,\gamma (1))$
,
$\Gamma ^{-1}\;:\;\pi _{1}^{\text{met}}(X,\gamma (0))\to \pi _{1}^{\text{met}}(X,\gamma (1))$
,
![]() $\Gamma ^{-1}([\beta ])= [\gamma ^{-}\ast \beta ]$
is non-expansive for the same reason (replacing
$\Gamma ^{-1}([\beta ])= [\gamma ^{-}\ast \beta ]$
is non-expansive for the same reason (replacing
![]() $\gamma$
with
$\gamma$
with
![]() $\gamma ^{-}$
). Thus,
$\gamma ^{-}$
). Thus,
![]() $\Gamma$
is an isometry.
$\Gamma$
is an isometry.
Theorem 4.12.
The
![]() $\pi _1$
-action
$\pi _1$
-action
![]() $\pi _{1}^{\text{met}}(X,x_0)\times \pi _{n}^{\text{met}}(X,x_0)\to \pi _{n}^{\text{met}}(X,x_0)$
given by
$\pi _{1}^{\text{met}}(X,x_0)\times \pi _{n}^{\text{met}}(X,x_0)\to \pi _{n}^{\text{met}}(X,x_0)$
given by
![]() $([\gamma ],[\alpha ])\mapsto [\gamma \ast \alpha ]$
is jointly continuous. Moreover,
$([\gamma ],[\alpha ])\mapsto [\gamma \ast \alpha ]$
is jointly continuous. Moreover,
![]() $\pi _{1}^{\text{met}}(X,x_0)$
acts on
$\pi _{1}^{\text{met}}(X,x_0)$
acts on
![]() $\pi _{n}^{\text{met}}(X,x_0)$
by isometry.
$\pi _{n}^{\text{met}}(X,x_0)$
by isometry.
Proof. That the action is by isometry follows immediately from Proposition 4.11. For continuity, suppose
![]() $\{g_k\}_{k\in \mathbb{N}}\to g$
in
$\{g_k\}_{k\in \mathbb{N}}\to g$
in
![]() $\pi _{1}^{\text{met}}(X,x_0)$
and
$\pi _{1}^{\text{met}}(X,x_0)$
and
![]() $\{a_k\}_{k\in \mathbb{N}}\to a$
in
$\{a_k\}_{k\in \mathbb{N}}\to a$
in
![]() $\pi _{n}^{\text{met}}(X,x_0)$
. Let
$\pi _{n}^{\text{met}}(X,x_0)$
. Let
![]() $\epsilon \gt 0$
. Find
$\epsilon \gt 0$
. Find
![]() $K\in \mathbb{N}$
such that
$K\in \mathbb{N}$
such that
![]() $\max \{\rho (g_k,g),\rho (a_k,a)\}\lt \epsilon/2$
for all
$\max \{\rho (g_k,g),\rho (a_k,a)\}\lt \epsilon/2$
for all
![]() $k\geq K$
. Thus for
$k\geq K$
. Thus for
![]() $k\geq K$
, there exist
$k\geq K$
, there exist
![]() $\gamma _k\in g_k$
and
$\gamma _k\in g_k$
and
![]() $\delta _k\in g$
with
$\delta _k\in g$
with
![]() $\mu (\gamma _k,\delta _k)\lt \epsilon/2$
and
$\mu (\gamma _k,\delta _k)\lt \epsilon/2$
and
![]() $\alpha _k\in a_k$
and
$\alpha _k\in a_k$
and
![]() $\beta _k\in a$
with
$\beta _k\in a$
with
![]() $\mu (\alpha _k,\beta _k)\lt \epsilon/2$
. Our definition of the action
$\mu (\alpha _k,\beta _k)\lt \epsilon/2$
. Our definition of the action
![]() $\ast$
of loops on
$\ast$
of loops on
![]() $n$
-loops using a fixed retraction
$n$
-loops using a fixed retraction
![]() $r$
ensures that
$r$
ensures that
![]() $\mu (\gamma _k\ast \alpha _k,\delta _k\ast \beta _k)\lt \epsilon/2$
. Since
$\mu (\gamma _k\ast \alpha _k,\delta _k\ast \beta _k)\lt \epsilon/2$
. Since
![]() $g_k\ast a_k=[\gamma _k\ast \alpha _k]$
and
$g_k\ast a_k=[\gamma _k\ast \alpha _k]$
and
![]() $g\ast a=[\delta _k\ast \beta _k]$
for all
$g\ast a=[\delta _k\ast \beta _k]$
for all
![]() $k\geq K$
, we have
$k\geq K$
, we have
![]() $\rho (g_k\ast a_k,g\ast a)\lt \epsilon$
. We conclude that
$\rho (g_k\ast a_k,g\ast a)\lt \epsilon$
. We conclude that
![]() $\{g_k\ast a_k\}_{k\in \mathbb{N}}\to g\ast a$
in
$\{g_k\ast a_k\}_{k\in \mathbb{N}}\to g\ast a$
in
![]() $\pi _{n}^{\text{met}}(X,x_0)$
.
$\pi _{n}^{\text{met}}(X,x_0)$
.
Finally, we compare the pseudometric topology to the quotient and
![]() $\tau$
-topologies.
$\tau$
-topologies.
Proposition 4.13.
The function
![]() $\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _{n}^{\text{met}}(X,x_0)$
,
$\pi \;:\;\Omega ^{n}(X,x_0)\to \pi _{n}^{\text{met}}(X,x_0)$
,
![]() $\pi (\alpha )=[\alpha ]$
is continuous. Thus, the topologies of
$\pi (\alpha )=[\alpha ]$
is continuous. Thus, the topologies of
![]() $\pi _{n}^{\text{qtop}}(X,x_0)$
and
$\pi _{n}^{\text{qtop}}(X,x_0)$
and
![]() $\pi _{n}^{\tau }(X,x_0)$
are at least as fine as that of
$\pi _{n}^{\tau }(X,x_0)$
are at least as fine as that of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
.
$\pi _{n}^{\text{met}}(X,x_0)$
.
Proof. Suppose
![]() $\{\alpha _k\}_{k\in \mathbb{N}}\to \alpha$
in
$\{\alpha _k\}_{k\in \mathbb{N}}\to \alpha$
in
![]() $\Omega ^{n}(X,x_0)$
and
$\Omega ^{n}(X,x_0)$
and
![]() $\epsilon \gt 0$
. There is an
$\epsilon \gt 0$
. There is an
![]() $K\in \mathbb{N}$
such that
$K\in \mathbb{N}$
such that
![]() $\mu (\alpha,\alpha _k)\lt \epsilon/2$
for
$\mu (\alpha,\alpha _k)\lt \epsilon/2$
for
![]() $k\geq K$
. Thus,
$k\geq K$
. Thus,
![]() $\rho ([\alpha ],[\alpha _k])\lt \epsilon$
for
$\rho ([\alpha ],[\alpha _k])\lt \epsilon$
for
![]() $k\geq K$
showing that
$k\geq K$
showing that
![]() $\{[\alpha _k]\}_{k\in \mathbb{N}}\to [\alpha ]$
in
$\{[\alpha _k]\}_{k\in \mathbb{N}}\to [\alpha ]$
in
![]() $\pi _{n}^{\text{met}}(X,x_0)$
. Thus,
$\pi _{n}^{\text{met}}(X,x_0)$
. Thus,
![]() $\pi$
is continuous. The second statement follows directly from the characterizations of the quotient and
$\pi$
is continuous. The second statement follows directly from the characterizations of the quotient and
![]() $\tau$
-topologies in Section 3.
$\tau$
-topologies in Section 3.
Remark 4.14.
Although basepoint-change isomorphisms are continuous when
![]() $\pi _n$
is given the quotient and
$\pi _n$
is given the quotient and
![]() $\tau$
-topologies, the
$\tau$
-topologies, the
![]() $\pi _1$
-action
$\pi _1$
-action
![]() $\pi _1(X,x)\times \pi _n(X,x)\to \pi _n(X,x)$
can be discontinuous when
$\pi _1(X,x)\times \pi _n(X,x)\to \pi _n(X,x)$
can be discontinuous when
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _n$
are given the quotient topology [10]. Apparently, it is unknown if the
$\pi _n$
are given the quotient topology [10]. Apparently, it is unknown if the
![]() $\pi _1$
-action
$\pi _1$
-action
![]() $\pi _1(X,x)\times \pi _n(X,x)\to \pi _n(X,x)$
is continuous in the
$\pi _1(X,x)\times \pi _n(X,x)\to \pi _n(X,x)$
is continuous in the
![]() $\tau$
-topology.
$\tau$
-topology.
5. Comparison with the shape topology
Lemma 5.1.
If
![]() $K$
is a finite polyhedron and
$K$
is a finite polyhedron and
![]() $n \geq 1$
, then
$n \geq 1$
, then
![]() $\pi _{n}^{\text{sh}}(K,x_0)$
is discrete.
$\pi _{n}^{\text{sh}}(K,x_0)$
is discrete.
Proof. If the compact metric space
![]() $(K,d)$
is the underlying space of a finite simplicial complex, then
$(K,d)$
is the underlying space of a finite simplicial complex, then
![]() $K$
admits a topologically compatible
$K$
admits a topologically compatible
![]() $CAT(1)$
metric
$CAT(1)$
metric
![]() $d^{\prime}$
[Reference Bridson and Haefliger13, Corollary 5.19]. Consequently there exists
$d^{\prime}$
[Reference Bridson and Haefliger13, Corollary 5.19]. Consequently there exists
![]() $\epsilon \gt 0$
so that for any space
$\epsilon \gt 0$
so that for any space
![]() $Y$
, if the maps
$Y$
, if the maps
![]() $f\;:\;Y\to K$
and
$f\;:\;Y\to K$
and
![]() $g\;:\;Y\to K$
are uniformly close with
$g\;:\;Y\to K$
are uniformly close with
![]() $d(f(y),g(y))\lt \epsilon$
for all
$d(f(y),g(y))\lt \epsilon$
for all
![]() $y \in Y$
, then
$y \in Y$
, then
![]() $f$
and
$f$
and
![]() $g$
are canonically homotopic via a homotopy
$g$
are canonically homotopic via a homotopy
![]() $H$
. The homotopy
$H$
. The homotopy
![]() $H$
maps
$H$
maps
![]() $f(y)$
to
$f(y)$
to
![]() $g(y)$
linearly with time, along the unique geodesic
$g(y)$
linearly with time, along the unique geodesic
![]() $[f(y),g(y)]$
in
$[f(y),g(y)]$
in
![]() $(K,d^{\prime})$
. The existence and continuity of
$(K,d^{\prime})$
. The existence and continuity of
![]() $H$
follow from Proposition 1.4 and Corollary 3.13 of [Reference Bridson and Haefliger13]. Thus,
$H$
follow from Proposition 1.4 and Corollary 3.13 of [Reference Bridson and Haefliger13]. Thus,
![]() $\pi _{n}^{\text{met}}(K,x_0)$
is discrete with the induced pseudometric generated by
$\pi _{n}^{\text{met}}(K,x_0)$
is discrete with the induced pseudometric generated by
![]() $d^{\prime}$
. Since
$d^{\prime}$
. Since
![]() $K$
is compact, Theorem 4.10 gives that the topology of
$K$
is compact, Theorem 4.10 gives that the topology of
![]() $\pi _{n}^{\text{met}}(K,x_0)$
is independent of the choice of metric on
$\pi _{n}^{\text{met}}(K,x_0)$
is independent of the choice of metric on
![]() $K$
. Hence,
$K$
. Hence,
![]() $\pi _{n}^{\text{met}}(K,x_0)$
is discrete with the induced pseudometric generated by
$\pi _{n}^{\text{met}}(K,x_0)$
is discrete with the induced pseudometric generated by
![]() $d$
.
$d$
.
Proposition 5.2.
If
![]() $X$
is a compact metric space, then the topology of
$X$
is a compact metric space, then the topology of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is at least as fine as that of
$\pi _{n}^{\text{met}}(X,x_0)$
is at least as fine as that of
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
.
$\pi _{n}^{\text{sh}}(X,x_0)$
.
Proof. Since
![]() $X$
is compact, we may construct
$X$
is compact, we may construct
![]() $\check{\pi }_{n}(X,x_0)$
by replacing
$\check{\pi }_{n}(X,x_0)$
by replacing
![]() ${\text{cov}}(X)$
with a cofinal sequence of finite covers. Whenever
${\text{cov}}(X)$
with a cofinal sequence of finite covers. Whenever
![]() $\mathscr{U}\in{\text{cov}}(X)$
is finite,
$\mathscr{U}\in{\text{cov}}(X)$
is finite,
![]() $|N(\mathscr{U})|$
is a finite polyhedron, and thus,
$|N(\mathscr{U})|$
is a finite polyhedron, and thus,
![]() $\pi _{n}^{\text{met}}(|N(\mathscr{U})|,U_0)$
is discrete by Lemma 5.1. Since
$\pi _{n}^{\text{met}}(|N(\mathscr{U})|,U_0)$
is discrete by Lemma 5.1. Since
![]() $X$
is compact, any canonical map
$X$
is compact, any canonical map
![]() $p_{\mathscr{U}}\;:\;X\to |N(\mathscr{U})|$
will be uniformly continuous and thus the induced homomorphism
$p_{\mathscr{U}}\;:\;X\to |N(\mathscr{U})|$
will be uniformly continuous and thus the induced homomorphism
![]() $p_{\mathscr{U}\#}\;:\;\pi _{n}^{\text{met}}(X,x_0)\to \pi _{n}^{\text{met}}(|N(\mathscr{U})|,U_0)$
will be continuous by Proposition 4.8. Since
$p_{\mathscr{U}\#}\;:\;\pi _{n}^{\text{met}}(X,x_0)\to \pi _{n}^{\text{met}}(|N(\mathscr{U})|,U_0)$
will be continuous by Proposition 4.8. Since
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
has the initial topology with respect to homomorphisms
$\pi _{n}^{\text{sh}}(X,x_0)$
has the initial topology with respect to homomorphisms
![]() $p_{\mathscr{U}\#}$
with discrete codomains, it follows that the topology of
$p_{\mathscr{U}\#}$
with discrete codomains, it follows that the topology of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is at least as fine as that of
$\pi _{n}^{\text{met}}(X,x_0)$
is at least as fine as that of
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
.
$\pi _{n}^{\text{sh}}(X,x_0)$
.
Remark 5.3.
The previous proposition fails when
![]() $X$
is no longer required to be compact. If
$X$
is no longer required to be compact. If
![]() $X=\mathbb{R}^{n+1}\backslash \{\bf{0}\}$
is punctured real
$X=\mathbb{R}^{n+1}\backslash \{\bf{0}\}$
is punctured real
![]() $(n+1)$
-space as in Example 4.9, then
$(n+1)$
-space as in Example 4.9, then
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is isomorphic to
$\pi _{n}^{\text{met}}(X,x_0)$
is isomorphic to
![]() $\mathbb{Z}$
with the indiscrete topology whereas
$\mathbb{Z}$
with the indiscrete topology whereas
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
is isomorphic to
$\pi _{n}^{\text{sh}}(X,x_0)$
is isomorphic to
![]() $\mathbb{Z}$
with the discrete topology.
$\mathbb{Z}$
with the discrete topology.
Definition 5.4.
Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\mathscr{U}$
be an open cover of
$\mathscr{U}$
be an open cover of
![]() $X$
. The
$X$
. The
![]() $n$
-th Spanier group of
$n$
-th Spanier group of
![]() $(X,x_0)$
with respect to
$(X,x_0)$
with respect to
![]() $\mathscr{U}$
is the subgroup
$\mathscr{U}$
is the subgroup
![]() $\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
of
$\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
of
![]() $\pi _n(X,x_0)$
generated by path-conjugates
$\pi _n(X,x_0)$
generated by path-conjugates
![]() $[\gamma \ast f]\in \pi _n(X,x_0)$
where
$[\gamma \ast f]\in \pi _n(X,x_0)$
where
![]() $\gamma \;:\;([0,1],0)\to (X,x_0)$
is a path and
$\gamma \;:\;([0,1],0)\to (X,x_0)$
is a path and
![]() $\alpha \;:\;(S^n,d_0)\to (X,\gamma (1))$
has image in
$\alpha \;:\;(S^n,d_0)\to (X,\gamma (1))$
has image in
![]() $U$
for some
$U$
for some
![]() $U\in \mathscr{U}$
. The
$U\in \mathscr{U}$
. The
![]() $n$
-th Spanier group of
$n$
-th Spanier group of
![]() $(X,x_0)$
is the intersection
$(X,x_0)$
is the intersection
![]() $\pi _{n}^{\text{Sp}}(X,x_0)=\bigcap _{\mathscr{U}\in{\text{cov}}(X)}\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
.
$\pi _{n}^{\text{Sp}}(X,x_0)=\bigcap _{\mathscr{U}\in{\text{cov}}(X)}\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
.
Spanier groups (in dimension
![]() $n=1$
) first appeared in [Reference Spanier22] and have been used frequently in the past decade. Higher Spanier groups were more recently introduced [Reference Akbar Bahredar, Kouhestani and Passandideh4]. Note that since Spanier groups
$n=1$
) first appeared in [Reference Spanier22] and have been used frequently in the past decade. Higher Spanier groups were more recently introduced [Reference Akbar Bahredar, Kouhestani and Passandideh4]. Note that since Spanier groups
![]() $\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
,
$\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
,
![]() ${\text{cov}}(X)$
are always normal subgroups of
${\text{cov}}(X)$
are always normal subgroups of
![]() $\pi _n(X,x_0)$
, the sets of left cosets
$\pi _n(X,x_0)$
, the sets of left cosets
![]() $\{[g]\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)\mid \mathscr{U}\in{\text{cov}}(X),[g]\in \pi _n(X,x_0)\}$
forms a basis for a topology on
$\{[g]\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)\mid \mathscr{U}\in{\text{cov}}(X),[g]\in \pi _n(X,x_0)\}$
forms a basis for a topology on
![]() $\pi _n(X,x_0)$
.
$\pi _n(X,x_0)$
.
Definition 5.5.
We refer to the topology on
![]() $\pi _n(Y,y_0)$
generated by cosets of the Spanier groups
$\pi _n(Y,y_0)$
generated by cosets of the Spanier groups
![]() $\pi _{n}^{\text{Sp}}(\mathscr{U},y_0)$
as the Spanier topology.
$\pi _{n}^{\text{Sp}}(\mathscr{U},y_0)$
as the Spanier topology.
In the current paper, the Spanier topology will not be studied in detail but will only serve as a convenient bound for the pseudometric topology. In order to make these comparisons, we recall known results that compare Spanier groups with homomorphisms
![]() $p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _n(|N(\mathscr{U})|,U_0)$
induced by canonical maps. The following has a straightforward proof. See [Reference Akbar Bahredar, Kouhestani and Passandideh4, Prop 4.13] or [Reference Aceti and Brazas3, Lemma 3.10].
$p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _n(|N(\mathscr{U})|,U_0)$
induced by canonical maps. The following has a straightforward proof. See [Reference Akbar Bahredar, Kouhestani and Passandideh4, Prop 4.13] or [Reference Aceti and Brazas3, Lemma 3.10].
Proposition 5.6.
For every
![]() $\mathscr{U}\in{\text{cov}}(X)$
and choice of canonical map
$\mathscr{U}\in{\text{cov}}(X)$
and choice of canonical map
![]() $p_{\mathscr{U}}\;:\;X\to |N(\mathscr{U})|$
, there exists a
$p_{\mathscr{U}}\;:\;X\to |N(\mathscr{U})|$
, there exists a
![]() $\mathscr{V}\in{\text{cov}}(X)$
such that
$\mathscr{V}\in{\text{cov}}(X)$
such that
![]() $\pi _{n}^{\text{Sp}}(\mathscr{V},x_0)\leq \ker (p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _n(|N(\mathscr{U})|,U_0))$
.
$\pi _{n}^{\text{Sp}}(\mathscr{V},x_0)\leq \ker (p_{\mathscr{U}\#}\;:\;\pi _n(X,x_0)\to \pi _n(|N(\mathscr{U})|,U_0))$
.
Since the shape topology on
![]() $\pi _n(X,x_0)$
is generated by left cosets of subgroups of the form
$\pi _n(X,x_0)$
is generated by left cosets of subgroups of the form
![]() $\ker (p_{\mathscr{U}\#})$
, we have the following.
$\ker (p_{\mathscr{U}\#})$
, we have the following.
Corollary 5.7 ([Reference Aceti and Brazas3], Remark 5.5). For any metrizable space
![]() $X$
, Spanier topology on
$X$
, Spanier topology on
![]() $\pi _n(X,x_0)$
is at least as fine as the shape topology.
$\pi _n(X,x_0)$
is at least as fine as the shape topology.
Determining when the Spanier topology agrees with the shape topology is a more technical matter that has been addressed in [Reference Aceti and Brazas3]. To state this properly, we recall the following definition.
Definition 5.8.
Let
![]() $n\geq 0$
. A topological space
$n\geq 0$
. A topological space
![]() $Y$
is
$Y$
is
![]() $LC^n$
at
$LC^n$
at
![]() $y\in Y$
if for every neighborhood
$y\in Y$
if for every neighborhood
![]() $U$
of
$U$
of
![]() $y$
, there exists a neighborhood
$y$
, there exists a neighborhood
![]() $V$
of
$V$
of
![]() $y$
such that
$y$
such that
![]() $V\subseteq U$
and such that for all
$V\subseteq U$
and such that for all
![]() $0\leq k\leq n$
, every map
$0\leq k\leq n$
, every map
![]() $f\;:\;S^k\to V$
extends to a map
$f\;:\;S^k\to V$
extends to a map
![]() $g\;:\;D^{k+1}\to U$
. We say
$g\;:\;D^{k+1}\to U$
. We say
![]() $Y$
is
$Y$
is
![]() $LC^n$
if
$LC^n$
if
![]() $Y$
is
$Y$
is
![]() $LC^n$
at all of its points.
$LC^n$
at all of its points.
The following lemma was proved in dimension
![]() $n=1$
in [Reference Brazas and Fabel12]. For
$n=1$
in [Reference Brazas and Fabel12]. For
![]() $n\geq 2$
, the proof requires other techniques from shape theory.
$n\geq 2$
, the proof requires other techniques from shape theory.
Lemma 5.9 ([Reference Aceti and Brazas3], Lemma 5.1). Suppose
![]() $X$
is
$X$
is
![]() $LC^{n-1}$
. Then for every
$LC^{n-1}$
. Then for every
![]() $\mathscr{U}\in{\text{cov}}(X)$
, there exists
$\mathscr{U}\in{\text{cov}}(X)$
, there exists
![]() $\mathscr{V}\in{\text{cov}}(X)$
such that for any canonical map
$\mathscr{V}\in{\text{cov}}(X)$
such that for any canonical map
![]() $p_{\mathscr{V}}\;:\;X\to |N(\mathscr{V})|$
, we have
$p_{\mathscr{V}}\;:\;X\to |N(\mathscr{V})|$
, we have
![]() $\ker (p_{\mathscr{V}\#}\;:\;\pi _n(X,x_0)\to \pi _n(N(\mathscr{V}),V_0))\leq \pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
.
$\ker (p_{\mathscr{V}\#}\;:\;\pi _n(X,x_0)\to \pi _n(N(\mathscr{V}),V_0))\leq \pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
.
Corollary 5.7 and Lemma 5.9 now combine to give the following.
Corollary 5.10.
If
![]() $X$
is a
$X$
is a
![]() $LC^{n-1}$
metrizable space, then the Spanier and shape topologies on
$LC^{n-1}$
metrizable space, then the Spanier and shape topologies on
![]() $\pi _n(X,x_0)$
agree.
$\pi _n(X,x_0)$
agree.
Next, we compare the Spanier topology and pseudometric topologies by comparing neighborhood bases at the identity element.
Proposition 5.11.
Let
![]() $(X,d)$
be a path-connected metric space. Then for every
$(X,d)$
be a path-connected metric space. Then for every
![]() $r\gt 0$
, there exists
$r\gt 0$
, there exists
![]() $\mathscr{U}\in{\text{cov}}(X)$
such that
$\mathscr{U}\in{\text{cov}}(X)$
such that
![]() $\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)\leq B_{\rho }(e,r)$
.
$\pi _{n}^{\text{Sp}}(\mathscr{U},x_0)\leq B_{\rho }(e,r)$
.
Proof. Given
![]() $r\gt 0$
, let
$r\gt 0$
, let
![]() $\mathscr{U}=\{B_d(x,r/2)\mid x\in X\}$
be the cover of
$\mathscr{U}=\{B_d(x,r/2)\mid x\in X\}$
be the cover of
![]() $X$
by
$X$
by
![]() $r/2$
-balls. Consider a generator
$r/2$
-balls. Consider a generator
![]() $[\alpha \ast f]\in \pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
where
$[\alpha \ast f]\in \pi _{n}^{\text{Sp}}(\mathscr{U},x_0)$
where
![]() $\alpha \;:\;([0,1],0)\to (X,x_0)$
is a path and
$\alpha \;:\;([0,1],0)\to (X,x_0)$
is a path and
![]() $f\;:\;(S^n,d_0)\to (X,\alpha (1))$
is a map with image in
$f\;:\;(S^n,d_0)\to (X,\alpha (1))$
is a map with image in
![]() $B_d(x,r/2)$
for some
$B_d(x,r/2)$
for some
![]() $x\in X$
. Let
$x\in X$
. Let
![]() $g\;:\;S^n\to X$
be the constant map at
$g\;:\;S^n\to X$
be the constant map at
![]() $\alpha (1)$
. Since
$\alpha (1)$
. Since
![]() $e=[\alpha \ast g]$
and
$e=[\alpha \ast g]$
and
![]() $\mu (\alpha \ast f,\alpha \ast g)\lt r$
, we have
$\mu (\alpha \ast f,\alpha \ast g)\lt r$
, we have
![]() $\rho ([\alpha \ast f],e)\lt r$
, giving
$\rho ([\alpha \ast f],e)\lt r$
, giving
![]() $[\alpha \ast f]\in B_{\rho }(e,r)$
.
$[\alpha \ast f]\in B_{\rho }(e,r)$
.
Corollary 5.12.
For a metric space
![]() $(X,d)$
, the Spanier topology on
$(X,d)$
, the Spanier topology on
![]() $\pi _n(X,x_0)$
is at least as fine as the pseudometric topology induced by
$\pi _n(X,x_0)$
is at least as fine as the pseudometric topology induced by
![]() $d$
.
$d$
.
At this point, we have sufficient results to prove Case (1) of Theorem 1.1. The following lemma addresses Case (2).
Lemma 5.13.
If
![]() $(X,d)$
is homeomorphic to an inverse limit
$(X,d)$
is homeomorphic to an inverse limit
![]() $\varprojlim _{j\in \mathbb{N}}(X_j,r_{j+1,j})$
of finite polyhedra
$\varprojlim _{j\in \mathbb{N}}(X_j,r_{j+1,j})$
of finite polyhedra
![]() $X_j$
where the bonding maps
$X_j$
where the bonding maps
![]() $r_{j+1,j}\;:\;X_{j+1}\to X_j$
are retractions, then for all
$r_{j+1,j}\;:\;X_{j+1}\to X_j$
are retractions, then for all
![]() $n\geq 1$
, the shape topology on
$n\geq 1$
, the shape topology on
![]() $\pi _n(X,x_0)$
is at least as fine as the pseudometric topology.
$\pi _n(X,x_0)$
is at least as fine as the pseudometric topology.
Proof. Identify
![]() $X=\varprojlim _{j\in \mathbb{N}}(X_j,r_{j+1,j})$
and let
$X=\varprojlim _{j\in \mathbb{N}}(X_j,r_{j+1,j})$
and let
![]() $r_j\;:\;X\to X_j$
,
$r_j\;:\;X\to X_j$
,
![]() $j\in \mathbb{N}$
denote the projection maps. Let
$j\in \mathbb{N}$
denote the projection maps. Let
![]() $s_{j,j+1}\;:\;X_j\to X_{j+1}$
be a section to
$s_{j,j+1}\;:\;X_j\to X_{j+1}$
be a section to
![]() $r_{j+1,j}$
. When
$r_{j+1,j}$
. When
![]() $i\gt j$
,
$i\gt j$
,
![]() $s_{j,i}=s_{i-1,i}\circ s_{i-2,i-1}\circ \cdots \circ s_{j,j+1}$
is a section to
$s_{j,i}=s_{i-1,i}\circ s_{i-2,i-1}\circ \cdots \circ s_{j,j+1}$
is a section to
![]() $r_{i,j}=r_{j,j+1}\circ \cdots \circ r_{i-2,i-2}\circ r_{i,i-1}$
. For fixed all pairs
$r_{i,j}=r_{j,j+1}\circ \cdots \circ r_{i-2,i-2}\circ r_{i,i-1}$
. For fixed all pairs
![]() $i,j\in \mathbb{N}$
, let
$i,j\in \mathbb{N}$
, let
![]() $t_{j,i}\;:\;X_j\to X_i$
be
$t_{j,i}\;:\;X_j\to X_i$
be
![]() $r_{j,i}$
if
$r_{j,i}$
if
![]() $j\gt i$
,
$j\gt i$
,
![]() $id_{X_j}$
if
$id_{X_j}$
if
![]() $i=j$
, and
$i=j$
, and
![]() $s_{j,i}$
if
$s_{j,i}$
if
![]() $j\lt i$
. Then, the maps
$j\lt i$
. Then, the maps
![]() $\{t_{j,i}\}_{i\in \mathbb{N}}$
induce a map
$\{t_{j,i}\}_{i\in \mathbb{N}}$
induce a map
![]() $t_j\;:\;X_j\to X$
which is a section to
$t_j\;:\;X_j\to X$
which is a section to
![]() $r_j$
. Thus, we may identify
$r_j$
. Thus, we may identify
![]() $X_1\subseteq X_2\subseteq X_3\subseteq \cdots$
as a nested sequence of closed subspaces of
$X_1\subseteq X_2\subseteq X_3\subseteq \cdots$
as a nested sequence of closed subspaces of
![]() $X$
where
$X$
where
![]() $\overline{\bigcup _{j\in \mathbb{N}}X_j}=X$
. In particular,
$\overline{\bigcup _{j\in \mathbb{N}}X_j}=X$
. In particular,
![]() $X_k$
consists of the sequences
$X_k$
consists of the sequences
![]() $(x_j)_{j\in \mathbb{N}}\in X$
where
$(x_j)_{j\in \mathbb{N}}\in X$
where
![]() $x_j=x_k$
for all
$x_j=x_k$
for all
![]() $j\geq k$
and
$j\geq k$
and
![]() $r_k((x_j)_{j\in \mathbb{N}})=(x_1,x_2,\dots,x_{k-1},x_k,x_k,x_k,\dots )$
for all
$r_k((x_j)_{j\in \mathbb{N}})=(x_1,x_2,\dots,x_{k-1},x_k,x_k,x_k,\dots )$
for all
![]() $(x_j)_{j\in \mathbb{N}}\in X$
.
$(x_j)_{j\in \mathbb{N}}\in X$
.
Pick basepoint
![]() $x_0\in X_1$
and fix
$x_0\in X_1$
and fix
![]() $n\geq 1$
. Let
$n\geq 1$
. Let
![]() $\delta \gt 0$
so that
$\delta \gt 0$
so that
![]() $B_{\rho }(e,\delta )$
is a basic neighborhood of the identity in
$B_{\rho }(e,\delta )$
is a basic neighborhood of the identity in
![]() $\pi _{n}^{\text{met}}(X,x_0)$
. Since
$\pi _{n}^{\text{met}}(X,x_0)$
. Since
![]() $X$
is compact, the sequence
$X$
is compact, the sequence
![]() $\{X_j\}_{j\in \mathbb{N}}$
gives an
$\{X_j\}_{j\in \mathbb{N}}$
gives an
![]() $\bf{HPol_{\ast }}$
-expansion of
$\bf{HPol_{\ast }}$
-expansion of
![]() $X$
, and therefore, the subgroups
$X$
, and therefore, the subgroups
![]() $H_j=\ker (r_{j\#}\;:\;\pi _n(X,x_0)\to \pi _n(X_j,x_0))$
form a neighborhood base at the identity in
$H_j=\ker (r_{j\#}\;:\;\pi _n(X,x_0)\to \pi _n(X_j,x_0))$
form a neighborhood base at the identity in
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
. To show that the shape topology is finer than (or equal to) the pseudometric topology, it suffices to show that there exists
$\pi _{n}^{\text{sh}}(X,x_0)$
. To show that the shape topology is finer than (or equal to) the pseudometric topology, it suffices to show that there exists
![]() $k\in \mathbb{N}$
such that
$k\in \mathbb{N}$
such that
![]() $H_k\subseteq B_{\rho }(e,\delta )$
.
$H_k\subseteq B_{\rho }(e,\delta )$
.
First, we claim that there exists
![]() $k\in \mathbb{N}$
such that
$k\in \mathbb{N}$
such that
![]() $d(x,r_k(x))\lt \frac{\delta }{2}$
for all
$d(x,r_k(x))\lt \frac{\delta }{2}$
for all
![]() $x\in X$
. By Theorem 4.10, we may alter the metric
$x\in X$
. By Theorem 4.10, we may alter the metric
![]() $d$
on
$d$
on
![]() $X$
without changing the topology of
$X$
without changing the topology of
![]() $\pi _{n}^{\text{met}}(X,x_0)$
. Since
$\pi _{n}^{\text{met}}(X,x_0)$
. Since
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
is a topological invariant, doing so will not change the topology of
$\pi _{n}^{\text{sh}}(X,x_0)$
is a topological invariant, doing so will not change the topology of
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
either. In particular, let
$\pi _{n}^{\text{sh}}(X,x_0)$
either. In particular, let
![]() $d_j$
be a metric inducing the topology of
$d_j$
be a metric inducing the topology of
![]() $X_j$
that is bounded by
$X_j$
that is bounded by
![]() $1$
. For elements
$1$
. For elements
![]() $x=(x_1,x_2,\dots )$
and
$x=(x_1,x_2,\dots )$
and
![]() $y=(y_1,y_2,\dots )$
of
$y=(y_1,y_2,\dots )$
of
![]() $\prod _{j=1}^{\infty }X_j$
, the formula
$\prod _{j=1}^{\infty }X_j$
, the formula
![]() $d(x,y)=\sum _{j=1}^{\infty }\frac{d_j(x_j,y_j)}{2^j}$
defines a metric that induces the topology of
$d(x,y)=\sum _{j=1}^{\infty }\frac{d_j(x_j,y_j)}{2^j}$
defines a metric that induces the topology of
![]() $\prod _{j=1}^{\infty }X_j$
with the product topology [Reference Engelking18, 4.2.2]. Since
$\prod _{j=1}^{\infty }X_j$
with the product topology [Reference Engelking18, 4.2.2]. Since
![]() $X$
is topologized a subspace of
$X$
is topologized a subspace of
![]() $\prod _{j=1}^{\infty }X_j$
,
$\prod _{j=1}^{\infty }X_j$
,
![]() $d(x,y)$
restricts to a metric that induces the topology of
$d(x,y)$
restricts to a metric that induces the topology of
![]() $X$
. Find
$X$
. Find
![]() $k\in \mathbb{N}$
such that
$k\in \mathbb{N}$
such that
![]() $\sum _{j=k+1}^{\infty }\frac{1}{2^j}\lt \frac{\delta }{2}$
. Then, for any
$\sum _{j=k+1}^{\infty }\frac{1}{2^j}\lt \frac{\delta }{2}$
. Then, for any
![]() $x=(x_1,x_2,\dots )\in X$
, we have
$x=(x_1,x_2,\dots )\in X$
, we have
This proves the desired claim.
Finally, we check that
![]() $H_k\subseteq B_{\rho }(e,\delta )$
. Given
$H_k\subseteq B_{\rho }(e,\delta )$
. Given
![]() $a\in H_k$
, find an
$a\in H_k$
, find an
![]() $n$
-loop
$n$
-loop
![]() $\alpha \in a$
. Then,
$\alpha \in a$
. Then,
![]() $\beta =r_k\circ \alpha$
is null-homotopic in
$\beta =r_k\circ \alpha$
is null-homotopic in
![]() $X_k$
and since
$X_k$
and since
![]() $X_k\subseteq X$
,
$X_k\subseteq X$
,
![]() $\beta$
is null-homotopic in
$\beta$
is null-homotopic in
![]() $X$
. Moreover, our choice of
$X$
. Moreover, our choice of
![]() $k$
ensures that
$k$
ensures that
![]() $d(\alpha ({\bf{t}}),\beta ({\bf{t})})=d(\alpha ({\bf{t}}),r_k(\alpha ({\bf{t}})))\lt \frac{\delta }{2}$
for all
$d(\alpha ({\bf{t}}),\beta ({\bf{t})})=d(\alpha ({\bf{t}}),r_k(\alpha ({\bf{t}})))\lt \frac{\delta }{2}$
for all
![]() ${\bf{t}}\in [0,1]^n$
. Thus
${\bf{t}}\in [0,1]^n$
. Thus
![]() $\mu (\alpha,\beta )\lt \frac{\delta }{2}$
. It follows that
$\mu (\alpha,\beta )\lt \frac{\delta }{2}$
. It follows that
![]() $\rho (a,e)\lt \delta$
, giving
$\rho (a,e)\lt \delta$
, giving
![]() $a\in B_{\rho }(e,\delta )$
. The inclusion
$a\in B_{\rho }(e,\delta )$
. The inclusion
![]() $H_J\subseteq B_{\rho }(e,\delta )$
follows.
$H_J\subseteq B_{\rho }(e,\delta )$
follows.
At this point, we have established all results needed to prove Theorem 1.1.
Proof of Theorem 1.1. Suppose
![]() $(X,d)$
is a compact metric space. By Proposition 5.2, the pseudometric topology is at least as fine as the shape topology (note that this is where compactness is required). To prove equivalence of the two topologies in Case (1), we assume
$(X,d)$
is a compact metric space. By Proposition 5.2, the pseudometric topology is at least as fine as the shape topology (note that this is where compactness is required). To prove equivalence of the two topologies in Case (1), we assume
![]() $X$
is
$X$
is
![]() $LC^{n-1}$
. By Corollary 5.12, the Spanier topology is at least as fine as the pseudometric topology. Thus, we have the following situation:
$LC^{n-1}$
. By Corollary 5.12, the Spanier topology is at least as fine as the pseudometric topology. Thus, we have the following situation:
Finally, Corollary 5.10 implies that the Spanier topology agrees with the shape topology. Thus, the pseudometric topology agrees with the shape topology. Equivalence in Case (2) follows directly from Lemma 5.13.
Remark 5.14.
The
![]() $LC^{n-1}$
condition in Case (1) of Theorem 1.1 implies the well-known
$LC^{n-1}$
condition in Case (1) of Theorem 1.1 implies the well-known
![]() $n$
-movability condition from shape theory [Reference Mardešić and Segal21, II§8.1, Theorem 6]. Moreover, the hypothesis in Case (2) of Theorem 1.1 directly implies that
$n$
-movability condition from shape theory [Reference Mardešić and Segal21, II§8.1, Theorem 6]. Moreover, the hypothesis in Case (2) of Theorem 1.1 directly implies that
![]() $X$
is
$X$
is
![]() $n$
-movable. However, Theorem 1.1 does not appear to generalize readily to
$n$
-movable. However, Theorem 1.1 does not appear to generalize readily to
![]() $n$
-movable spaces. Indeed, the main structure of interest is the homotopy group
$n$
-movable spaces. Indeed, the main structure of interest is the homotopy group
![]() $\pi _n(X,x_0)$
itself, rather than an
$\pi _n(X,x_0)$
itself, rather than an
![]() $\bf{HPol_{\ast }}$
-expansion or the shape-type of
$\bf{HPol_{\ast }}$
-expansion or the shape-type of
![]() $X$
. In general, movability conditions allow one to lift maps inductively along an inverse system. However, for the standard shape category these lifts are only lifts up to homotopy. One must be able to obtain strict lifts in order to induce a map to the limit.
$X$
. In general, movability conditions allow one to lift maps inductively along an inverse system. However, for the standard shape category these lifts are only lifts up to homotopy. One must be able to obtain strict lifts in order to induce a map to the limit.
Next, we consider an example where the equivalence of the shape topology and pseudometric topology allows one to characterize the pseudometric topology by appealing to the simpler shape-theoretic setting.
Example 5.15 (Earring mapping tori). Fix
![]() $n\geq 2$
. The
$n\geq 2$
. The
![]() $n$
-dimensional infinite earring space is
$n$
-dimensional infinite earring space is
![]() $\mathbb{E}_n=\bigcup _{k\in \mathbb{N}}C_k$
where
$\mathbb{E}_n=\bigcup _{k\in \mathbb{N}}C_k$
where
![]() $C_k\subseteq \mathbb{R}^{n+1}$
is the
$C_k\subseteq \mathbb{R}^{n+1}$
is the
![]() $n$
-sphere of radius
$n$
-sphere of radius
![]() $1/k$
centered at
$1/k$
centered at
![]() $(1/k,0,0,\dots,0)$
[17]. Sometimes this space is referred to as the Barratt-Milnor Spheres [6]. It is known that
$(1/k,0,0,\dots,0)$
[17]. Sometimes this space is referred to as the Barratt-Milnor Spheres [6]. It is known that
![]() $\mathbb{E}_n$
is
$\mathbb{E}_n$
is
![]() $(n-1)$
-connected, locally
$(n-1)$
-connected, locally
![]() $(n-1)$
-connected (and thus
$(n-1)$
-connected (and thus
![]() $LC^{n-1}$
), and
$LC^{n-1}$
), and
![]() $\pi _n(\mathbb{E}_n,\bf{0})\cong \mathbb{Z}^{\mathbb{N}}$
[17]. Let
$\pi _n(\mathbb{E}_n,\bf{0})\cong \mathbb{Z}^{\mathbb{N}}$
[17]. Let
![]() $f\;:\;\mathbb{E}_n\to \mathbb{E}_n$
be the canonical based “shift map” that maps
$f\;:\;\mathbb{E}_n\to \mathbb{E}_n$
be the canonical based “shift map” that maps
![]() $C_k$
homeomorphically to
$C_k$
homeomorphically to
![]() $C_{k+1}$
for all
$C_{k+1}$
for all
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $T_f=\mathbb{E}_n\times [0,1]/\mathord{\sim }$
,
$T_f=\mathbb{E}_n\times [0,1]/\mathord{\sim }$
,
![]() $(x,0)\sim (f(x),1)$
be the mapping torus of
$(x,0)\sim (f(x),1)$
be the mapping torus of
![]() $f$
(See Figure 1
). Then,
$f$
(See Figure 1
). Then,
![]() $T_f$
is an
$T_f$
is an
![]() $n+1$
-dimensional Peano continuum. Take the image of the origin to be the basepoint
$n+1$
-dimensional Peano continuum. Take the image of the origin to be the basepoint
![]() $x_0$
. The group
$x_0$
. The group
![]() $\pi _n(T_f,x_0)$
is uncountable but its elements have a fairly simple characterization [Reference Aceti and Brazas3, Example 5.3]. We use Theorem 1.1 to characterize the pseudometric topology on
$\pi _n(T_f,x_0)$
is uncountable but its elements have a fairly simple characterization [Reference Aceti and Brazas3, Example 5.3]. We use Theorem 1.1 to characterize the pseudometric topology on
![]() $\pi _n(T_f,x_0)$
. Since
$\pi _n(T_f,x_0)$
. Since
![]() $T_f$
is shape equivalent to the aspherical space
$T_f$
is shape equivalent to the aspherical space
![]() $S^1$
, the
$S^1$
, the
![]() $n$
-th shape homotopy group
$n$
-th shape homotopy group
![]() $\check{\pi }_n(T_f,x_0)$
is trivial. Thus,
$\check{\pi }_n(T_f,x_0)$
is trivial. Thus,
![]() $\pi _{n}^{\text{sh}}(T_f,x_0)$
is an indiscrete group. Given a point
$\pi _{n}^{\text{sh}}(T_f,x_0)$
is an indiscrete group. Given a point
![]() $x\in T_f$
, either
$x\in T_f$
, either
![]() $T_f$
is locally contractible at
$T_f$
is locally contractible at
![]() $x$
or
$x$
or
![]() $x$
admits a neighborhood that deformation retracts onto a subspace that is homeomorphic to
$x$
admits a neighborhood that deformation retracts onto a subspace that is homeomorphic to
![]() $\mathbb{E}_n$
. Since
$\mathbb{E}_n$
. Since
![]() $\mathbb{E}^n$
is
$\mathbb{E}^n$
is
![]() $LC^{n-1}$
, it follows that
$LC^{n-1}$
, it follows that
![]() $T_f$
is
$T_f$
is
![]() $LC^{n-1}$
. It then follows from Case (1) of Theorem 1.1 that the topology of
$LC^{n-1}$
. It then follows from Case (1) of Theorem 1.1 that the topology of
![]() $\pi _{n}^{\text{met}}(T_f,x_0)$
agrees with the shape topology and is therefore indiscrete.
$\pi _{n}^{\text{met}}(T_f,x_0)$
agrees with the shape topology and is therefore indiscrete.
Figure 1. The mapping torus of the shift map
![]() $f\;:\;\mathbb{E}_2\to \mathbb{E}_2$
of the
$f\;:\;\mathbb{E}_2\to \mathbb{E}_2$
of the
![]() $2$
-dimensional earring space.
$2$
-dimensional earring space.
We also consider an example showing that Theorem 1.1 fails to hold in any dimension
![]() $n\geq 1$
without the local path-connectedness hypothesis, i.e. the assumption that
$n\geq 1$
without the local path-connectedness hypothesis, i.e. the assumption that
![]() $X$
is
$X$
is
![]() $LC^{0}$
.
$LC^{0}$
.
Example 5.16.
Fix
![]() $n\geq 1$
. Let
$n\geq 1$
. Let
![]() $A_0=\{0\}\times [\!-\!1,1]\subseteq \mathbb{R}^2$
and
$A_0=\{0\}\times [\!-\!1,1]\subseteq \mathbb{R}^2$
and
![]() $A_1=\{(x,\sin (1/x))\in \mathbb{R}^2\mid 0\lt x\leq 1/\pi \}$
so that
$A_1=\{(x,\sin (1/x))\in \mathbb{R}^2\mid 0\lt x\leq 1/\pi \}$
so that
![]() $A=A_0\cup A_1$
is the closed topologists sine curve. Let
$A=A_0\cup A_1$
is the closed topologists sine curve. Let
![]() $a_0=(0,1)\in A_0$
and
$a_0=(0,1)\in A_0$
and
![]() $a_1=(1/\pi,0)\in A_1$
. Consider the quotient space
$a_1=(1/\pi,0)\in A_1$
. Consider the quotient space
![]() $B=A\times S^n/\{a_1\}\times S^n$
with quotient map
$B=A\times S^n/\{a_1\}\times S^n$
with quotient map
![]() $q:A\times S^n\to B$
(See Figure 2
) and let
$q:A\times S^n\to B$
(See Figure 2
) and let
![]() $C=q(A_0\times S^n)$
be the cylinder over
$C=q(A_0\times S^n)$
be the cylinder over
![]() $S^n$
. Set
$S^n$
. Set
![]() $x_0=q(a_0,d_0)$
and
$x_0=q(a_0,d_0)$
and
![]() $x_1=q(\{a_1\}\times S^n)$
. For each
$x_1=q(\{a_1\}\times S^n)$
. For each
![]() $a\in A$
, let
$a\in A$
, let
![]() $\ell _a:S^n\to B$
be the map
$\ell _a:S^n\to B$
be the map
![]() $\ell _a(t)=q(a,t)$
, which is an embedding when
$\ell _a(t)=q(a,t)$
, which is an embedding when
![]() $a\neq a_1$
and constant at
$a\neq a_1$
and constant at
![]() $x_1$
if
$x_1$
if
![]() $a=a_1$
. Note that
$a=a_1$
. Note that
![]() $\ell _a$
is null-homotopic if and only if
$\ell _a$
is null-homotopic if and only if
![]() $a\in A_1$
. Construct the space
$a\in A_1$
. Construct the space
![]() $X$
by attaching an arc
$X$
by attaching an arc
![]() $[0,1]$
to
$[0,1]$
to
![]() $B$
by identifying
$B$
by identifying
![]() $0\sim x_0$
and
$0\sim x_0$
and
![]() $1\sim x_1$
. We metrize
$1\sim x_1$
. We metrize
![]() $X$
with the canonical quotient metric. The space
$X$
with the canonical quotient metric. The space
![]() $X$
is a compact metric space, which may be embedded in
$X$
is a compact metric space, which may be embedded in
![]() $\mathbb{R}^{n+2}$
. However,
$\mathbb{R}^{n+2}$
. However,
![]() $X$
is not
$X$
is not
![]() $LC^0$
at any point in
$LC^0$
at any point in
![]() $C$
. Note that
$C$
. Note that
![]() $\pi _n(X,x_0)$
is infinite cyclic generated by
$\pi _n(X,x_0)$
is infinite cyclic generated by
![]() $[\ell _{a_0}]$
. However,
$[\ell _{a_0}]$
. However,
![]() $X$
is shape equivalent to the aspherical space
$X$
is shape equivalent to the aspherical space
![]() $S^1$
and the
$S^1$
and the
![]() $n$
-th shape homomorphism
$n$
-th shape homomorphism
![]() $\Psi \;:\;\pi _n(X,x_0)\to \check{\pi }_n(X,x_0)$
is the trivial homomorphism for all
$\Psi \;:\;\pi _n(X,x_0)\to \check{\pi }_n(X,x_0)$
is the trivial homomorphism for all
![]() $n\geq 1$
(the domain and codomain are both
$n\geq 1$
(the domain and codomain are both
![]() $\mathbb{Z}$
in the case
$\mathbb{Z}$
in the case
![]() $n=1$
). Therefore,
$n=1$
). Therefore,
![]() $\pi _{n}^{\text{sh}}(X,x_0)$
is indiscrete.
$\pi _{n}^{\text{sh}}(X,x_0)$
is indiscrete.
Figure 2. The space
![]() $B$
in the case
$B$
in the case
![]() $n=1$
is the union of a cylinder over
$n=1$
is the union of a cylinder over
![]() $S^1$
and a non-compact surface that limits on the cylinder. The space
$S^1$
and a non-compact surface that limits on the cylinder. The space
![]() $X$
is constructed by connecting the two path components with an arc.
$X$
is constructed by connecting the two path components with an arc.
On the other hand, we check that
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is discrete. Let
$\pi _{n}^{\text{met}}(X,x_0)$
is discrete. Let
![]() $Y$
be the union of the cylinder
$Y$
be the union of the cylinder
![]() $C$
and the added arc. Then
$C$
and the added arc. Then
![]() $Y$
is a compact polyhedron homotopy equivalent to
$Y$
is a compact polyhedron homotopy equivalent to
![]() $S^n$
and so
$S^n$
and so
![]() $\pi _{n}^{\text{met}}(Y,x_0)$
is discrete. Therefore, there exists an
$\pi _{n}^{\text{met}}(Y,x_0)$
is discrete. Therefore, there exists an
![]() $\epsilon \gt 0$
such that if a based map
$\epsilon \gt 0$
such that if a based map
![]() $f\;:\;S^n\to Y$
is
$f\;:\;S^n\to Y$
is
![]() $\epsilon$
-close to some null-homotopic based map (in the uniform metric), then
$\epsilon$
-close to some null-homotopic based map (in the uniform metric), then
![]() $f$
is null-homotopic. Choose such an
$f$
is null-homotopic. Choose such an
![]() $\epsilon$
which is also less than one-third of the diameter of the attached arc. Thus, an
$\epsilon$
which is also less than one-third of the diameter of the attached arc. Thus, an
![]() $\epsilon$
-neighborhood of
$\epsilon$
-neighborhood of
![]() $x_1$
(the endpoint of the arc) is disjoint from
$x_1$
(the endpoint of the arc) is disjoint from
![]() $C$
. Now suppose
$C$
. Now suppose
![]() $f\;:\;S^n\to X$
is a null-homotopic based map and that
$f\;:\;S^n\to X$
is a null-homotopic based map and that
![]() $g\;:\;S^n\to X$
is
$g\;:\;S^n\to X$
is
![]() $\epsilon$
-close to
$\epsilon$
-close to
![]() $f$
. Define
$f$
. Define
![]() $f^{\prime}\;:\;S^n\to X$
to agree with
$f^{\prime}\;:\;S^n\to X$
to agree with
![]() $f$
on
$f$
on
![]() $f^{-1}(Y)$
and to map
$f^{-1}(Y)$
and to map
![]() $f^{-1}(X\backslash Y)$
to
$f^{-1}(X\backslash Y)$
to
![]() $x_1$
. We define
$x_1$
. We define
![]() $g^{\prime}$
similarly for
$g^{\prime}$
similarly for
![]() $g$
. It’s easy to see that
$g$
. It’s easy to see that
![]() $f\simeq f^{\prime}$
,
$f\simeq f^{\prime}$
,
![]() $g\simeq g^{\prime}$
, and that
$g\simeq g^{\prime}$
, and that
![]() $f^{\prime},g^{\prime}$
are
$f^{\prime},g^{\prime}$
are
![]() $\epsilon$
-close maps in
$\epsilon$
-close maps in
![]() $Y$
. Therefore,
$Y$
. Therefore,
![]() $f^{\prime}\simeq g^{\prime}$
in
$f^{\prime}\simeq g^{\prime}$
in
![]() $Y$
. We conclude that
$Y$
. We conclude that
![]() $g$
is null-homotopic in
$g$
is null-homotopic in
![]() $X$
. This proves that
$X$
. This proves that
![]() $\pi _{n}^{\text{met}}(X,x_0)$
is discrete.
$\pi _{n}^{\text{met}}(X,x_0)$
is discrete.
In the next example, we illustrate an application of Case (2) of Theorem 1.1 as an important situation where Case (1) does not apply.
Example 5.17.
Let
![]() $K_1,K_2,K_3,\cdots$
be a sequence of based, compact polyhedra and
$K_1,K_2,K_3,\cdots$
be a sequence of based, compact polyhedra and
![]() $X_k=\bigvee _{j=1}^{k}K_j$
for
$X_k=\bigvee _{j=1}^{k}K_j$
for
![]() $k\in \mathbb{N}$
. We take
$k\in \mathbb{N}$
. We take
![]() $r_{k+1,k}\;:\;X_{k+1}\to X_k$
to be the retraction which collapses
$r_{k+1,k}\;:\;X_{k+1}\to X_k$
to be the retraction which collapses
![]() $K_{k+1}$
to the basepoint and
$K_{k+1}$
to the basepoint and
![]() $X=\varprojlim _{k\in \mathbb{N}}(X_k,r_{k+1,k})$
. Then
$X=\varprojlim _{k\in \mathbb{N}}(X_k,r_{k+1,k})$
. Then
![]() $X=\widetilde{\bigvee }_{j\in \mathbb{N}}K_j$
is a Peano continuum, which we refer to as the shrinking wedge of the sequence
$X=\widetilde{\bigvee }_{j\in \mathbb{N}}K_j$
is a Peano continuum, which we refer to as the shrinking wedge of the sequence
![]() $\{K_j\}_{j\in \mathbb{N}}$
. Since
$\{K_j\}_{j\in \mathbb{N}}$
. Since
![]() $X$
is an inverse limit of a nested sequence of polyhedral retracts, Case (2) of Theorem 1.1 implies that for any choice of metric
$X$
is an inverse limit of a nested sequence of polyhedral retracts, Case (2) of Theorem 1.1 implies that for any choice of metric
![]() $d$
on
$d$
on
![]() $X$
,
$X$
,
![]() $\pi _{n}^{\text{met}}(X,x_0)=\pi _{n}^{\text{sh}}(X,x_0)$
for all
$\pi _{n}^{\text{met}}(X,x_0)=\pi _{n}^{\text{sh}}(X,x_0)$
for all
![]() $n\geq 1$
. For example, the
$n\geq 1$
. For example, the
![]() $m$
-dimensional earring space
$m$
-dimensional earring space
![]() $\mathbb{E}_m$
is homeomorphic to
$\mathbb{E}_m$
is homeomorphic to
![]() $\widetilde{\bigvee }_{j\in \mathbb{N}}S^m$
and the conclusion
$\widetilde{\bigvee }_{j\in \mathbb{N}}S^m$
and the conclusion
![]() $\pi _{n}^{\text{met}}(\mathbb{E}_m,x_0)=\pi _{n}^{\text{sh}}(\mathbb{E}_m,x_0)$
only follows from Case (1) of Theorem 1.1 when
$\pi _{n}^{\text{met}}(\mathbb{E}_m,x_0)=\pi _{n}^{\text{sh}}(\mathbb{E}_m,x_0)$
only follows from Case (1) of Theorem 1.1 when
![]() $n\leq m$
. Interestingly, this equivalence of topologies holds even when infinitely many
$n\leq m$
. Interestingly, this equivalence of topologies holds even when infinitely many
![]() $K_j$
fail to be
$K_j$
fail to be
![]() $m$
-connected, in which case
$m$
-connected, in which case
![]() $X$
is not
$X$
is not
![]() $LC^{m}$
and the algebraic structure of
$LC^{m}$
and the algebraic structure of
![]() $\pi _n(X,x_0)$
is complicated significantly by Whitehead products.
$\pi _n(X,x_0)$
is complicated significantly by Whitehead products.
We conclude by considering the special case of the fundamental group where covering spaces and their generalizations are typically useful.
Corollary 5.18.
For a Peano continuum
![]() $X$
and
$X$
and
![]() $x_0\in X$
, the following are equivalent:
$x_0\in X$
, the following are equivalent:
-
1.
 $\rho$
is a metric on
$\rho$
is a metric on
 $\pi _1(X,x)$
,
$\pi _1(X,x)$
, -
2.
 $X$
is
$X$
is
 $\pi _1$
-shape injective,
$\pi _1$
-shape injective,
-
3. for every
 $[\alpha ]\in \pi _1(X,x)$
, there exists a covering map
$[\alpha ]\in \pi _1(X,x)$
, there exists a covering map
 $p:(E,e)\to (X,x_0)$
such that
$p:(E,e)\to (X,x_0)$
such that
 $[\alpha ]\notin p_{\#}(\pi _1(E,e))$
, i.e
$[\alpha ]\notin p_{\#}(\pi _1(E,e))$
, i.e
 $\alpha$
lifts to a non-loop in
$\alpha$
lifts to a non-loop in
 $E$
.
$E$
.
Proof. The equivalence (2)
![]() $\Leftrightarrow$
(3) was proved in [Reference Brazas and Fabel12]. (1)
$\Leftrightarrow$
(3) was proved in [Reference Brazas and Fabel12]. (1)
![]() $\Rightarrow$
(2) if
$\Rightarrow$
(2) if
![]() $\rho$
is a metric, then
$\rho$
is a metric, then
![]() $\pi _{1}^{\text{met}}(X,x_0)$
is Hausdorff. Since
$\pi _{1}^{\text{met}}(X,x_0)$
is Hausdorff. Since
![]() $\pi _{1}^{\text{met}}(X,x_0)= \pi _{1}^{\text{sh}}(X,x_0)$
by Theorem 1.1,
$\pi _{1}^{\text{met}}(X,x_0)= \pi _{1}^{\text{sh}}(X,x_0)$
by Theorem 1.1,
![]() $\pi _{1}^{\text{sh}}(X,x_0)$
is Hausdorff and it follows that
$\pi _{1}^{\text{sh}}(X,x_0)$
is Hausdorff and it follows that
![]() $\Psi _1\;:\;\pi _{1}(X,x_0)\to \check{\pi }_{1}(X,x_0)$
is injective. (2)
$\Psi _1\;:\;\pi _{1}(X,x_0)\to \check{\pi }_{1}(X,x_0)$
is injective. (2)
![]() $\Rightarrow$
(1) If
$\Rightarrow$
(1) If
![]() $\Psi _1\;:\;\pi _{1}(X,x_0)\to \check{\pi }_{1}(X,x_0)$
is injective, then
$\Psi _1\;:\;\pi _{1}(X,x_0)\to \check{\pi }_{1}(X,x_0)$
is injective, then
![]() $\pi _{1}^{\text{met}}(X,x_0)=\pi _{1}^{\text{sh}}(X,x_0)$
is Hausdorff. Since the topology of
$\pi _{1}^{\text{met}}(X,x_0)=\pi _{1}^{\text{sh}}(X,x_0)$
is Hausdorff. Since the topology of
![]() $\pi _{1}^{\text{met}}(X,x_0)$
is generated by the pseudometric
$\pi _{1}^{\text{met}}(X,x_0)$
is generated by the pseudometric
![]() $\rho$
,
$\rho$
,
![]() $\rho$
is a metric.
$\rho$
is a metric.
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.