Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-04T19:24:23.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplier systems for Hilbert's and Siegel's modular groups

Published online by Cambridge University Press:  18 May 2009

Karl-Bernhard Gundlach
Karl-Bernhard Gundlach
Affiliation:
Fachbereich Mathematik Der Universität Marburg Lahnberge, 3550 Marburg/Lahn, Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical generalizations (already investigated in the second half of last century) of the modular group SL(2, ℤ) are the groups ГK = SL(2, o)(o the principal order of a totally real number field K, [K:ℚ]=n), operating, originally, on a product 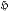of n upper half-planes or, for n=2, on the product 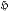1×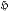− of an upper and a lower half-plane by

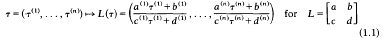
(where v(i), for v∈K, denotes the jth conjugate of v), and Гn = Sp(n, ℤ), operating on 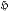n={Z∣Z=X+iY∈ℂ(n,n),tZ=Z, Y>0} by

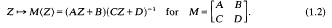
Nowadays ГK is called Hilbert's modular group of K and Гn Siegel's modular group of degree (or genus) n. For n=1 we have Гℚ=Г1= SL(2, ℤ). The functions corresponding to modular forms and modular functions for SL(2, ℤ) and its subgroups are holomorphic (or meromorphic) functions with an invariance property of the form

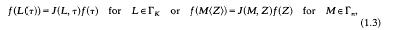
J(L, t) for fixed L (or J(M, Z) for fixed M) denoting a holomorphic function without zeros on 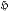) (or on 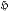n). A function J;, defined on ℤK×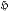or ℤn×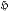n to be able to appear in (1.3) with f≢0, has to satisfy certain functional equations (see below, (2.3)–(2.5) for ГK, (5.7)–(5.9) for Гn) and is called an automorphic factor (AF) then. In close analogy to the case n=1, mainly AFs of the following kind have been used:

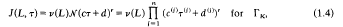
with a complex number r, the weight of J, and complex numbers v(L), v(M). AFs of this kind are called classical automorphic factors (CAP) in the sequel. If r∉ℤ, the values of the function v on ГK (or Гn) depend on the branch of (…)r. For a fixed choice of the branch (for each L∈ГK or M∈Гn) the functional equations for J, by (1.4), (1.5), correspond to functional equations for v. A function v satisfying those equations is called a multiplier system (MS) of weight r for ГK (or Гn).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 27 , October 1985 , pp. 57 - 80
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Christian, U., Über Hilbert-Siegelsche Modulformen und Poincarésche Reihen, Math. Ann. 148 (1962), 257–307.Google Scholar
2.Endres, R., Multiplikatorsysteme der symplektischen Thetagruppe, Monatsh. Math. 94 (1982), 281–297.CrossRefGoogle Scholar
3.Freitag, E., Automorphy factors of Hilbert's modular group, Discrete subgroups of Lie groups and applications to moduli (Internat. Colloq., Bombay, 1973) (Oxford Univ. Press, 1975) 9–19.Google Scholar
4.Grosche, J., Bemerkungen über Multiplikatoren von Modulformen zu Kongruenzgruppen der Hilbert-Siegelschen Modulgruppe, Acta Arith. 33 (1977), 187–193.CrossRefGoogle Scholar
5.Gundlach, K.-B., Zusammenhänge zwischen Modulformen in einer und in zwei Variablen, Nachr. Akad. Wiss. Göttingen II: Math. Phys. Kl. (1965), 47–88.Google Scholar
6.Gundlach, K.-B., Die Bestimmung der Funktionen zu einigen Hilbertschen Modulgruppen, J. Reine Angew. Math. 220 (1965), 109–153.Google Scholar
7.Gundlach, K.-B., Nullstellen Hilbertscher Modulformen, Nachr. Akad. Wiss. Göttingen II: Math. Phys. Kl. (1981), 1–38.Google Scholar
8.Kirchheimer, F., Zur Bestimmung der linearen Charaktere symplektischer Hauptkongruenz-untergruppen, Math. Z. 150 (1976), 135–148.CrossRefGoogle Scholar
9.MaaB, H., Zur Theorie der automorphen Funktionen von n Veränderlichen, Math. Ann. 117 (1940), 538–578.Google Scholar
10.MaaB, H., Modulformen und quadratische Formen über dem quadratischen Zahlkörper R(√5), Math. Ann. 118 (1941), 65–84.Google Scholar
11.MaaB, H., Die Multiplikatorsysteme zur Siegelschen Modulgruppe, Nachr. Akad. Wiss. Göttingen II: Math. Phys. Kl. (1964), 125–135.Google Scholar
12.Petersson, H., Automorphe Formen als metrische Invarianten I, Math. Nachr. 1 (1948), 158–212.CrossRefGoogle Scholar
13.Rankin, R. A., Modular forms and functions (Cambridge University Press, 1977).CrossRefGoogle Scholar