Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ricceri, Biagio
2008.
Pareto Optimality, Game Theory And Equilibria.
Vol. 17,
Issue. ,
p.
23.
Ricceri, Biagio
2009.
A three critical points theorem revisited.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 9,
p.
3084.
El Manouni, Said
2011.
A study of nonlinear problems for the -Laplacian in via Ricceri’s principle.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 13,
p.
4496.
Cammaroto, F.
and
Vilasi, L.
2013.
On a Schrödinger–Kirchhoff-type equation involving the -Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 81,
Issue. ,
p.
42.


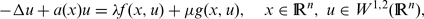
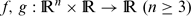 are Carathéodory functions, λ and μ two positive parameters.
are Carathéodory functions, λ and μ two positive parameters.