Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-02T23:56:47.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Modulus of nearly uniform smoothness and Lindenstrauss formulae

Published online by Cambridge University Press:  18 May 2009

Tomás Domínguez Benavides
Tomás Domínguez Benavides
Affiliation:
Departamento de Ańalisis Matemàtico, Universidad de Sevilla, Apdo.1160, 41080-Sevilla, Spain.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Lindenstrauss formula

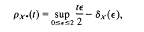
which states a strong relationship between the (Clarkson) modulus of uniform convexity δx of a Banach space X and the modulus of uniform smoothness px* of the conjugate space X*, is well known. Following the idea of the definitions of nearly uniform smooth space by S. Prus and modulus of uniform smoothness we define a modulus of nearly uniform smoothness and prove some Lindenstrauss type formulae concerning this modulus and the modulus of nearly uniform convexity for some measures of noncompactness.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 37 , Issue 2 , May 1995 , pp. 143 - 153
Copyright
Copyright © Glasgow Mathematical Journal Trust 1995

References

REFERENCES

1.de Reyna, J. Arias and Benavides, T. Dominguez, On a measure of noncompactness in Banach spaces with Schauder basis, Bollettino. U.M.I. 7A (1993), 77–86.Google Scholar
2.Ayerbe, J. M. and Benavides, T. Dominguez, Connections between some Banach space coefficients concerning normal structure, J. Math. Anal. Appl. 172 (1993), 53–61.CrossRefGoogle Scholar
3.Banas, J., On modulus of noncompact convexity and its properties, Canad. Math. Bull. 30 (1987), 186–192.CrossRefGoogle Scholar
4.Banas, J., Compactness conditions in the geometric theory of Banach spaces, Nonlin. Anal. 16 (1991), 669–682.CrossRefGoogle Scholar
5.Bynum, W. L., Normal structure coefficients for Banach spaces, Pacific J. Math. 86 (1980), 427–435.CrossRefGoogle Scholar
6.Benavides, T. Dominguez, Some properties of the set and ball measures of noncompactness and applications, J. London Math. Soc. 34(2) (1986), 120–128.CrossRefGoogle Scholar
7.Benavides, T. Dominguez and Acedo, G. Lòpez, Lower bounds for normal structure coefficients, Proc. Roy. Soc. Edinburgh.Sect. A 121 (1992), 245–252.CrossRefGoogle Scholar
8.Goebel, K. and Sekowski, T., The modulus of noncompact convexity, Ann. Univ. Marie Curie Sklodowska. Sect A XXXVIII, 3 (1984), 41–48.Google Scholar
9.Huff, R., Banach spaces which are nearly uniformly convex, Rocky Mountain J. Math. 4 (1980), 743–749.Google Scholar
10.Partington, J. P., On nearly uniformly convex Banach spaces, Math. Proc. Camb. Phil. Soc. 93 (1983), 127–129.CrossRefGoogle Scholar
11.Prus, S., On Bynum's fixed point theorem, Atti. Sem. Mat. Fis. Univ. Modena 38 (1990), 535–545.Google Scholar
12.Prus, S., Nearly uniformly smooth Banach spaces, Bollettino U.M.I. 3(7) (1989), 507–521.Google Scholar
13.Sekowski, T. and Stachura, A., Noncompact smoothness and noncompact convexity, Atti. Sem. Mat. Fis. Univ. Modena 36 (1988), 329–338.Google Scholar