Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T07:57:16.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Modules over polycyclic groups have many irreducible images

Published online by Cambridge University Press:  18 May 2009

Kenneth A. Brown
Kenneth A. Brown
Affiliation:
Department Of Mathematics, University of Glasgow, Glasgow Scotland G12 8Qw
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recall that a Noetherian ring R is a Hilbert ring if the Jacobson radical of every factor ring of R is nilpotent. As one of the main results of [13], J. E. Roseblade proved that if J is a commutative Hilbert ring and G is a polycyclic-by-finite group then JG is a Hilbert ring. The main theorem of this paper is a generalisation of this result in the case where all the field images of J are absolute fields—we shall say that J is absolutely Hilbert. The result is stated in terms of the (Gabriel–Rentschler–) Krull dimension; the definition and basic properties of this may be found in [5]. Let M be a finitely generated right module over the ring R. We write AnnR(M) (or just Ann(M)) for the ideal {r ∈ R: Mr = 0}, the annihilator of M in R. If M is also a left module, its left annihilator will be denoted l-AnnR(M). If R is a group ring JG, put

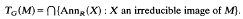
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 22 , Issue 2 , July 1981 , pp. 141 - 150
Copyright
Copyright © Glasgow Mathematical Journal Trust 1981

References

REFERENCES

1.Boratyński, M., A change of rings theorem and the Artin-Rees property, Proc. Amer. Math. Soc. 53 (1975), 307–310.CrossRefGoogle Scholar
2.Brown, K. A., Module extensions over Noetherian rings, to appear in J. Algebra.Google Scholar
3.Brown, K. A., Lenagan, T. H. and Stafford, J. T., K-theory and stable structure of some Noetherian group rings, Proc. London Math. Soc., (3) 42 (1981), 193–230.CrossRefGoogle Scholar
4.Duflo, M., Certaines algebres de type fini sont des algebres de Jacobson, J. Algebra 27 (1973), 358–365.CrossRefGoogle Scholar
5.Gordon, R. and Robson, J. C., Krull dimension, Mem. Amer. Math. Soc. 133 (1973).Google Scholar
6.Harper, D. L., Primitive irreducible representations of polycyclic groups, Ph.D. dissertation, Queen's College, Cambridge (1977).CrossRefGoogle Scholar
7.Jategaonkar, A. V., Integral group rings of polycyclic-by-finite groups, J. Pure Appl. Algebra 4 (1974), 337–343.CrossRefGoogle Scholar
8.Jategaonkar, A. V., Injective modules and localization in noncommutative Noetherian rings, Trans. Amer. Math. Soc. 190 (1974), 109–123.CrossRefGoogle Scholar
9.Müller, B. J., Localisation in non-commutative Noetherian rings, Canad. J. Math. 28 (1976), 600–610.CrossRefGoogle Scholar
10.Musson, I. M., Injective models for group rings of polycyclic groups II, Quart, J. Math. (2) 31 (1980), 449–466.CrossRefGoogle Scholar
11.Musson, I. M., Uniserial modules over enveloping algebras, unpublished note.Google Scholar
12.Passman, D. S., The algebraic structure of group rings (Interscience, 1977).Google Scholar
13.Roseblade, J. E., Group rings of polycyclic groups, J. Pure Appl. Algebra 3 (1973), 307–328.CrossRefGoogle Scholar
14.Roseblade, J. E., Prime ideals in group rings of polycyclic groups, Proc. London Math. Soc. (3) 36 (1978), 385–447.CrossRefGoogle Scholar
15.Roseblade, J. E. and Smith, P. F., A note on hypercentral group rings, J. London Math. Soc. (2) 13 (1976), 183–190.CrossRefGoogle Scholar
16.Segal, D., On the residual simplicity of certain modules, Proc. London Math. Soc. (3) 34 (1977), 327–353.CrossRefGoogle Scholar