Article contents
Models for joint isometries
Published online by Cambridge University Press: 18 May 2009
Extract
An N-tuple ℐ= (T1…, TN) of commuting contractions on a Hilbert space H is said to be a joint isometry if 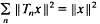 for all x in H, or, equivalently, if
for all x in H, or, equivalently, if 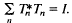 Athavale in [1] characterized the joint isometries as subnormal N-tuples whose minimal normal extensions have joint spectra in the unit sphere S2N−X a geometric perspective of this is given in [4]. Subsequently, V. Müller and F.-H. Vasilescu proved that commuting N-tuples which are joint contractions, i.e.
Athavale in [1] characterized the joint isometries as subnormal N-tuples whose minimal normal extensions have joint spectra in the unit sphere S2N−X a geometric perspective of this is given in [4]. Subsequently, V. Müller and F.-H. Vasilescu proved that commuting N-tuples which are joint contractions, i.e. 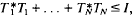 , can be represented as restrictions of certain weighted shifts direct sum a joint isometry. In this paper we adapt the canonical models of [3], and also construct a new canonical model, which completes the previous descriptions by showing joint isometries are indeed restrictions of specific multivariable weighted shifts [2].
, can be represented as restrictions of certain weighted shifts direct sum a joint isometry. In this paper we adapt the canonical models of [3], and also construct a new canonical model, which completes the previous descriptions by showing joint isometries are indeed restrictions of specific multivariable weighted shifts [2].
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1996
References
REFERENCES
- 1
- Cited by


