Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-02T23:43:19.275Z Has data issue: false hasContentIssue false
  • English
  • Français

A Mayer-Vietoris sequence in group homology and the decomposition of relation modules

Published online by Cambridge University Press:  18 May 2009

A. J. Duncan ,
Graham J. Ellis  and
N. D. Gilbert
A. J. Duncan
Affiliation:
Department of Mathematics & Statistics, University of Newcastle upon Tyne, Newcastle upon Tyne NEL 7RU, England
Graham J. Ellis
Affiliation:
Department of Mathematics, Unversity College, Galway, Ireland
N. D. Gilbert
Affiliation:
Department of Mathematical Sciences, Durham University, Science Laboratories, South Road, Durham DHI 3LE, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

W. A. Bogley and M. A. Gutierrez [2] have recently obtained an eight-term exact homology sequence that relates the integral homology of a quotient group Г/MN, where M and N are normal subgroups of the group Г, to the integral homology of the free product Г/M * Г/N in dimensions ≤3 by means of connecting terms constructed from commutator subgroups of Г, M, N and M ∩ N. In this paper we use the methods of [4] to recover this exact sequence under weaker hypotheses and for coefficients in 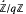/q for any non-negative integer q. Further, for q = 0 we extend the sequence by three terms in order to capture the relation between the fourth homology groups.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 37 , Issue 2 , May 1995 , pp. 159 - 171
Copyright
Copyright © Glasgow Mathematical Journal Trust 1995

References

REFERENCES

1.Bogley, W. A., An embedding for π2 of a subcomplex of a finite contractible two-complex. Glasgow Math. J. 33 (1991), 365–372.CrossRefGoogle Scholar
2.Bogley, W. A. and Gutierrez, M. A., Mayer-Vietoris sequences in homotopy of 2-complexes and in homology of groups. J. Pure Appl. Algebra 77 (1992), 39–65.CrossRefGoogle Scholar
3.Bogley, W. A. and Pride, S. J., Calculating generators of π2, in Two-dimensional Homotopy and Combinatorial Group Theory, Hog-Angeloni, C. et al. (Eds.). London Math. Soc. Lecture Notes 197, Cambridge University Press (1993).Google Scholar
4.Brown, R. and Ellis, G. J., Hopf formulae for the higher homology of a group. Bull. London Math. Soc. 20 (1988) 124–128.CrossRefGoogle Scholar
5.Brown, R. and Loday, J.-L., Theorems, Van Kampen for diagrams of spaces. Topology 26 (1987) 311–335.CrossRefGoogle Scholar
6.Duncan, A. J. and Howie, J., Weinbaum's conjecture on unique subwords of non-periodic words. Proc. Amer. Math. Soc. 115 (1992) 947–954.Google Scholar
7.Ellis, G. J., Relative derived functors and the homology of groups. Cahiers Top. Geom. Diff. 31(2) (1990) 121–135.Google Scholar
8.Ellis, G. J. and Steiner, R., Higher-dimensional crossed modules and the homotopy groups of (n + l)-ads. J. Pure Appl. Algebra 46 (1987) 117–136.CrossRefGoogle Scholar
9.Gilbert, N. D., Identities between sets of relations. J. Pure Appl. Algebra 83 (1993) 263–276.CrossRefGoogle Scholar
10.Gruenberg, K. W., Relation Modules of Finite Groups. CBMS Monograph 25 (American Mathematical Society, Providence RI, 1976).CrossRefGoogle Scholar
11.Gutierrez, M. A. and Ratcliffe, J. G., On the second homotopy group. Quart. J. Math. Oxford (2) 32 (1981) 45–55.CrossRefGoogle Scholar
12.Hilton, P. J. and Stammbach, U., A Course in Homological Algebra, (Springer-Verlag, Berlin-Heidelberg-New York 1971).CrossRefGoogle Scholar
13.Howie, J., Cohomology of one-relator products of locally indicable groups. J. London Math. Soc. (2) 30 (1984) 419–430.CrossRefGoogle Scholar
14.Howie, J., The quotient of a free product of groups by a single high-powered relator. I. Pictures. Fifth and higher powers. Proc. London Math. Soc. (3) 59 (1989) 507–540. Corrigendum. Proc. London Math. Soc. (3) 66 (1993) 538.CrossRefGoogle Scholar
15.Howie, J., The quotient of a free product of groups by a single high-powered relator. II. Fourth powers. Proc. London Math. Soc. (3) 61 (1990) 33–62.CrossRefGoogle Scholar
16.Huebschmann, J., Aspherical 2-complexes and an unsettled problem of J. H. C. Whitehead. Math. Ann. 258 (1981) 17–37.CrossRefGoogle Scholar
17.Linnell, P. A., Decomposition of augmentation ideals and relation modules. Proc. London Math. Soc. (3) 47 (1983) 83–127.CrossRefGoogle Scholar
18.Miller, C., The second homology of a group: relations between commutators. Proc. Amer. Math. Soc. 3 (1952) 588–595.CrossRefGoogle Scholar
19.Whitehead, J. H. C., A certain exact sequence. Ann. of Math. 52 (1950) 51–110.CrossRefGoogle Scholar