Article contents
Matrix invariants and complete intersections
Published online by Cambridge University Press: 18 May 2009
Extract
Consider the vector space of m-tuples of n by n matrices
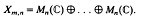 .
.
The linear group GLn(C) acts on Xm, n by simultaneous conjugation. The corresponding ring of polynomial invariants
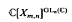
will be denoted by C(n, m) and is called the ring of matrix invariants of m-tuples of n by n matrices. C. Procesi has shown in [8] that C(n, m) is generated by traces of products of the corresponding generic matrices and, as such, coincides with the center of the trace ring of m generic n by n matrices R (n, m) which is also the ring of equivariant maps from Xm, n to Mn(ℂ).
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1990
References
REFERENCES
- 8
- Cited by


