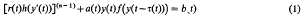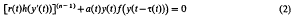Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Lu-San
and
Yeh, Cheh-Chih
1981.
Necessary and sufficient conditions for asymptotic decay of oscillations in delayed functional equations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 91,
Issue. 1-2,
p.
135.
Graef, John R
1983.
Nonoscillation of higher order functional differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 92,
Issue. 2,
p.
524.
Pachpatte, B.G
1997.
ON LEVIN TYPE COMPARISON THEOREMS FOR CERTAIN SECOND ORDER DIFFERENTIAL EQUATIONS.
Acta Mathematica Scientia,
Vol. 17,
Issue. 1,
p.
51.
Valdés, Juan E. Nápoles
2002.
On the Behavior of Some Second Order Nonlinear Differential Equations.
Results in Mathematics,
Vol. 41,
Issue. 3-4,
p.
337.
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
485.
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
565.
Saker, Samir H.
and
Gupta, Chaitan
2012.
Lyapunov′s Type Inequalities for Fourth‐Order Differential Equations.
Abstract and Applied Analysis,
Vol. 2012,
Issue. 1,
Saker, SH
Agarwal, RP
and
O’Regan, D
2012.
New gaps between zeros of fourth-order differential equations via Opial inequalities.
Journal of Inequalities and Applications,
Vol. 2012,
Issue. 1,
Graef, John R.
and
Hill, Mary
2015.
Nonoscillation of all solutions of a higher order nonlinear delay dynamic equation on time scales.
Journal of Mathematical Analysis and Applications,
Vol. 423,
Issue. 2,
p.
1693.
Saker, S. H.
and
Kubiaczyk, I.
2016.
Distribution of zeros and disconjugacy of fourth order differential equations.
Mathematische Nachrichten,
Vol. 289,
Issue. 1,
p.
97.
Abdeljawad, Thabet
Agarwal, Ravi P.
Alzabut, Jehad
Jarad, Fahd
and
Özbekler, Abdullah
2018.
Lyapunov-type inequalities for mixed non-linear forced differential equations within conformable derivatives.
Journal of Inequalities and Applications,
Vol. 2018,
Issue. 1,
Agarwal, Ravi P.
Bohner, Martin
and
Özbekler, Abdullah
2021.
Lyapunov Inequalities and Applications.
p.
1.