Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T19:26:58.205Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL NEGATIVITY OF SURFACES WITH NON-NEGATIVE KODAIRA DIMENSION AND TRANSVERSAL CONFIGURATIONS OF CURVES

Part of: Singularities Cycles and subschemes Discrete geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  18 January 2019

ROBERTO LAFACE  and
PIOTR POKORA Open the ORCID record for PIOTR POKORA [Opens in a new window]
ROBERTO LAFACE
Affiliation:
Technische Universität München, Zentrum Mathematik—M11, Boltzmannstrasse 3, 85748 Garching bei München, Germany e-mail: [email protected]
PIOTR POKORA*
Affiliation:
Institut für Algebraische Geometrie, Leibniz Universität Hannover, Welfengarten 1, D-30167 Hannover, Germany e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a bound on the H-constants of configurations of smooth curves having transversal intersection points only on an algebraic surface of non-negative Kodaira dimension. We also study in detail configurations of lines on smooth complete intersections 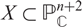$X \subset \mathbb{P}_{\mathbb{C}}^{n + 2}$ of multi-degree d = (d1, …, dn), and we provide a sharp and uniform bound on their H-constants, which only depends on d.

MSC classification

Primary: 14C20: Divisors, linear systems, invertible sheaves
Secondary: 14J70: Hypersurfaces 52C35: Arrangements of points, flats, hyperplanes 32S22: Relations with arrangements of hyperplanes
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 1 , January 2020 , pp. 123 - 135
Copyright
Copyright © Glasgow Mathematical Journal Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Present address: Piotr Pokora, Institute of Mathematics of the Polish Academy of Sciences, Śniadeckich 8, PL-00-656 Warsaw, Poland

References

Th. Bauer, S. Di Rocco, B. Harbourne, Huizenga, J., Lundman, A., Pokora, P. and Szemberg, T., Bounded negativity and arrangements of lines, Int. Math. Res. Not. 2015 (2015), 9456–9471.CrossRefGoogle Scholar
Th. Bauer, B. Harbourne, Knutsen, A. L., Küronya, A., Müller–Stach, S., Roulleau, X. and Szemberg, T., Negative curves on algebraic surfaces, Duke Math. J. 162 (2013), 1877–1894.CrossRefGoogle Scholar
Birkenhake, C. and Lange, H., Complex Abelian Varieties, Grundlehren der Mathematischen Wissenschaften, vol. 302, 2nd augmented edition (Springer, Berlin, 2004), xii+635. ISBN 3-540-20488-1/hbk.CrossRefGoogle Scholar
Harbourne, B., The geometry of rational surfaces and Hilbert functions of points in the plane, Can. Math. Soc. Conf. Proc. 6 (1986), 95–111.Google Scholar
Laface, R. and Pokora, P., On the local negativity of surfaces with numerically trivial canonical class, Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 29(2) (2018), 237–253.CrossRefGoogle Scholar
Miyaoka, Y., The maximal number of quotient singularities on surfaces with given numerical invariants, Math. Ann. 268 (1984), 159–171.CrossRefGoogle Scholar
Pokora, P., Harbourne constants and arrangements of lines on smooth hypersurfaces in $\mathbb{P}_{\mathbb{C}}^{3}$, Taiwanese J. Math. 20(1) (2016), 25–31.CrossRefGoogle Scholar
Pokora, P., Szemberg, T. and Roulleau, X., Bounded negativity, Harbourne constants and transversal arrangements of curves, Ann. Inst. Fourier 67(6) (2017), 2719–2735.CrossRefGoogle Scholar
Roulleau, X., Bounded negativity, Miyaoka-Sakai inequality and elliptic curve configurations, Int. Math. Res. Not. 2017(8) (2017), 2480–2496.Google Scholar
Urzúa, G., Arrangements of rational sections over curves and the varieties they define, Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 22(4) (2011), 453–486.CrossRefGoogle Scholar