Article contents
The lattice of inverse subsemigroups of a reduced inverse semigroup†
Published online by Cambridge University Press: 18 May 2009
Extract
An inverse semigroup R is said to be reduced (or proper) if ℛ∩σ= i (where σ is the minimum group congruence on R). McAlister has shown ([3], [4]) that every reduced inverse semigroup is isomorphic with a “P-semigroup” P(G, 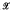 ,
, 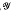 ), for some semilattice
), for some semilattice 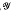 , poset
, poset 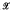 containing
containing 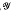 as an ideal, and group G acting on
as an ideal, and group G acting on 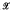 by order-automorphisms; (and, conversely, every P-semigroup is reduced). In [4], he also found the morphisms between P-semigroups, in terms of morphisms between the respective groups, and between the respective posets.
by order-automorphisms; (and, conversely, every P-semigroup is reduced). In [4], he also found the morphisms between P-semigroups, in terms of morphisms between the respective groups, and between the respective posets.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1976
References
REFERENCES
- 3
- Cited by


