Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T08:17:41.962Z Has data issue: false hasContentIssue false
  • English
  • Français

Jacobians for Measures in Coset Spaces

Published online by Cambridge University Press:  18 May 2009

S. Świerczkowski
S. Świerczkowski
Affiliation:
The University Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact topological group, let H be a closed subgroup and let G/H be the space of left cosets 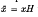= xH with the natural topology. We denote by μ a non-negative measure in G/Hdefined on the ring of Baire sets. G acts by left multiplication as a transitive group of homeomorphisms on G/H: Every t ∈ G defines the homeomorphism 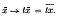We write, for E ⊂ G/H, tE = 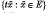. The measure μ is called stable (cf. [3], [4]) if from t ∈ G, E ⊂ G/H and μ(E) = 0 follows μ(tE) = 0. We say that μ is locally finite [3], [5] if every set of positive measure contains a subset of positive finite measure.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 4 , Issue 4 , September 1960 , pp. 208 - 212
Copyright
Copyright © Glasgow Mathematical Journal Trust 1960

References

1.Halmos, P. R., Measure theory, New York 1951.Google Scholar
2.Macbeath, A. M. and Świerczkowski, S., Measures in homogeneous spaces, Fundamenta Math., 49 (1960), 15–24.CrossRefGoogle Scholar
3.Macbeath, A. M. and Świerczkowski, S., Inherited measures; to appear in Proc. Roy. Soc. Edinburgh.Google Scholar
4.Świerczkowski, S., Measures equivalent to the Haar measure, Proc. Glasgow Math. Assoc., 4 (1960), 157–162.CrossRefGoogle Scholar
5.Zaanen, A. C., A note on measure theory, Nieuw Arch. Wisk. (3) 6 (1958), 58–65.Google Scholar