Article contents
ISOMORPHIC INDUCED MODULES AND DYNKIN DIAGRAM AUTOMORPHISMS OF SEMISIMPLE LIE ALGEBRAS
Published online by Cambridge University Press: 21 July 2015
Abstract
Consider a simple Lie algebra 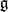 $\mathfrak{g}$ and
$\mathfrak{g}$ and 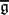 $\overline{\mathfrak{g}}$ ⊂
$\overline{\mathfrak{g}}$ ⊂ 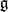 $\mathfrak{g}$ a Levi subalgebra. Two irreducible
$\mathfrak{g}$ a Levi subalgebra. Two irreducible 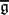 $\overline{\mathfrak{g}}$-modules yield isomorphic inductions to
$\overline{\mathfrak{g}}$-modules yield isomorphic inductions to 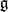 $\mathfrak{g}$ when their highest weights coincide up to conjugation by an element of the Weyl group W of
$\mathfrak{g}$ when their highest weights coincide up to conjugation by an element of the Weyl group W of 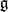 $\mathfrak{g}$ which is also a Dynkin diagram automorphism of
$\mathfrak{g}$ which is also a Dynkin diagram automorphism of 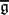 $\overline{\mathfrak{g}}$. In this paper, we study the converse problem: given two irreducible
$\overline{\mathfrak{g}}$. In this paper, we study the converse problem: given two irreducible 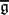 $\overline{\mathfrak{g}}$-modules of highest weight μ and ν whose inductions to
$\overline{\mathfrak{g}}$-modules of highest weight μ and ν whose inductions to 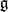 $\mathfrak{g}$ are isomorphic, can we conclude that μ and ν are conjugate under the action of an element of W which is also a Dynkin diagram automorphism of
$\mathfrak{g}$ are isomorphic, can we conclude that μ and ν are conjugate under the action of an element of W which is also a Dynkin diagram automorphism of 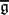 $\overline{\mathfrak{g}}$? We conjecture this is true in general. We prove this conjecture in type A and, for the other root systems, in various situations providing μ and ν satisfy additional hypotheses. Our result can be interpreted as an analogue for branching coefficients of the main result of Rajan [6] on tensor product multiplicities.
$\overline{\mathfrak{g}}$? We conjecture this is true in general. We prove this conjecture in type A and, for the other root systems, in various situations providing μ and ν satisfy additional hypotheses. Our result can be interpreted as an analogue for branching coefficients of the main result of Rajan [6] on tensor product multiplicities.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2015
References
REFERENCES
- 1
- Cited by


