Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Choe, Boo Rim
and
Rim, Kyung Soo
1996.
Fractional derivatives of Bloch functions, growth rate, and interpolation.
Acta Mathematica Hungarica,
Vol. 72,
Issue. 1-2,
p.
67.
Choe, Boo Rim
and
Yi, Heungsu
1998.
Representations and interpolations of harmonic Bergman functions on half-spaces.
Nagoya Mathematical Journal,
Vol. 151,
Issue. ,
p.
51.
Jihuai, Shi
and
Hua, Liu
2004.
Interpolating sequences for the fractral derivatives of Bloch functions in several variables.
Complex Variables, Theory and Application: An International Journal,
Vol. 49,
Issue. 14,
p.
1035.
Nam, Kyesook
2006.
Representations and Interpolations of Weighted Harmonic Bergman Functions.
Rocky Mountain Journal of Mathematics,
Vol. 36,
Issue. 1,
Tugores, Francesc
2010.
Interpolation of bounded sequences.
Czechoslovak Mathematical Journal,
Vol. 60,
Issue. 2,
p.
513.
Liu, Junming
Lou, Zengjian
and
Xiong, Chengji
2012.
Essential norms of integral operators on spaces of analytic functions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 13,
p.
5145.
Perfekt, Karl-Mikael
2013.
Duality and distance formulas in spaces defined by means of oscillation.
Arkiv för Matematik,
Vol. 51,
Issue. 2,
p.
345.
TUGORES, Francesc
and
TUGORES, Laia
2016.
ZERO-INTERPOLATING SEQUENCES.
Kyushu Journal of Mathematics,
Vol. 70,
Issue. 2,
p.
259.
Tugores, F.
and
Tugores, L.
2017.
Interpolation by derivatives in
$${H^\infty}$$
H
∞
.
Acta Mathematica Hungarica,
Vol. 153,
Issue. 2,
p.
265.
Tugores, F.
2017.
Reducing Sequences.
Ukrainian Mathematical Journal,
Vol. 69,
Issue. 2,
p.
325.
Tugores, Francesc
2018.
Recursive interpolating sequences.
Open Mathematics,
Vol. 16,
Issue. 1,
p.
461.
Tugores, Francesc
and
Tugores, Laia
2019.
A Note on Interpolation in Hardy Spaces.
Bulletin of the Iranian Mathematical Society,
Vol. 45,
Issue. 2,
p.
607.
Blasco, Oscar
Galindo, Pablo
Lindström, Mikael
and
Miralles, Alejandro
2019.
Interpolating sequences for weighted spaces of analytic functions on the unit ball of a Hilbert space.
Revista Matemática Complutense,
Vol. 32,
Issue. 1,
p.
115.
Li, Songxiao
Liu, Junming
and
Yuan, Cheng
2020.
Embedding Theorems for Dirichlet Type Spaces.
Canadian Mathematical Bulletin,
Vol. 63,
Issue. 1,
p.
106.
Qian, Ruishen
and
Zhu, Xiangling
2021.
Embedding of Dirichlet type spaces
into tent spaces and Volterra operators.
Canadian Mathematical Bulletin,
Vol. 64,
Issue. 3,
p.
697.
Miralles, Alejandro
and
Maletzki, Mario P.
2022.
On interpolating sequences for Bloch type spaces.
Journal of Mathematical Analysis and Applications,
Vol. 511,
Issue. 1,
p.
126079.
Miralles, Alejandro
and
Maletzki, Mario P.
2023.
The Constant of Interpolation in Bloch Type Spaces.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 6,
Miralles, Alejandro
2023.
Bounded below composition operators on the space of Bloch functions on the unit ball of a Hilbert space.
Banach Journal of Mathematical Analysis,
Vol. 17,
Issue. 4,
Miralles, Alejandro
2024.
Lipschitz continuity of the dilation of Bloch functions on the unit ball of a Hilbert space and applications.
Annals of Functional Analysis,
Vol. 15,
Issue. 2,


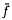 acting on the Bergman space is shown to be equivalent to
acting on the Bergman space is shown to be equivalent to 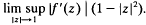 .
.