Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-12T01:46:07.999Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals Involving a Modified Bessel Function of the Second Kind and an E-Function

Published online by Cambridge University Press:  18 May 2009

T. M. Macrobert
T. M. Macrobert
Affiliation:
University of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The first formula to be proved is

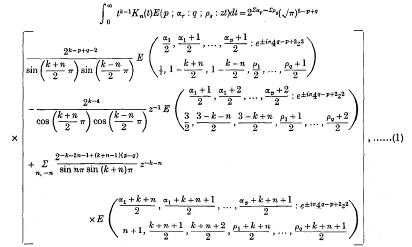
where p ≧ q + 1, | amp z | < л, R(k±n + αr)>0, r = l, 2, …, p. For other values of p and q the result is valid if the integral is convergent. A second formula is given in § 3.

The following formulae are required in the proof:

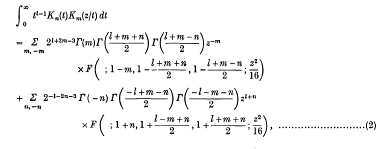
where R(z);>0, (1);

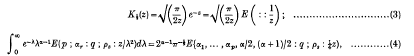
where R(α)>0, | amp z | < л, (2);

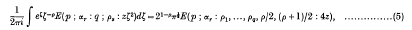
where the contour starts from -∞ on the ξ-axis, passes round the origin in the positive direction, and ends at -∞ on the ξ-axis, the initial value of amp ζ being - л, (3).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 2 , Issue 2 , October 1954 , pp. 93 - 96
Copyright
Copyright © Glasgow Mathematical Journal Trust 1954

References

REFERENCES

(1)MacRobert, T. M., Proc. Glasg. Math. Ass., 1 (1953), p. 187.CrossRefGoogle Scholar
(2),(3)MacRobert, T. M., Proc. Glasg. Math. Ass., 1 (1953), p. 191.Google Scholar
(4)Ragab, F. M., Proc. Glasg. Math. Ass., 2 (1954), p. 85.CrossRefGoogle Scholar