Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-02T21:13:05.280Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral operators involving Whittaker functions

Published online by Cambridge University Press:  18 May 2009

C. Nasim
C. Nasim
Affiliation:
Department of Mathematics, The University of Calgary, Calgary, Alberta Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

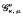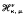We define the integral operators and as

and

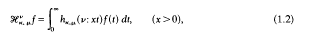
where

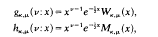
and Wk, u and Mk, u are the Whittaker's confluent hyper-geometric functions. These operators, in their slightly less general form, have been dealt with in [2] and [4]. There the authors have used the fact that these integral operators can be expressed as compositions of the Kober's fractional integral operators and the modified Laplace operator. Then these operators are inverted accordingly. Generally, this type of technique has been very useful for inverting many kinds of integral equations; and a good account of the procedures involved is given [5].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 2 , July 1983 , pp. 139 - 148
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Erdélyi, A. et al. , Tables of integral transforms, Vol. II, Batemann Manuscript Project, (McGraw-Hill, 1954).Google Scholar
2.Habibullah, G. H., A note on a pair of integral operators involving Whittaker's functions, Glasgow Math. J. 18 (1977), 99–100.CrossRefGoogle Scholar
3.Nasim, C., An inversion formula for a class of integral transforms, J. Math. Anal. Appl. 52 (1975), 525–537.CrossRefGoogle Scholar
4.Saxena, R. K., An inversion formula for the Varma transform”, Proc. Cambridge Philos. Soc., 62 (1966), 467–471.CrossRefGoogle Scholar
5.Sneddon, I. N., Mixed boundary value problems in potential theory, (North-Holland, 1966).Google Scholar
6.Titchmarsh, E. C., The theory of Fourier integrals, Second Edition (Oxford University Press, 1948).Google Scholar
7.Widder, D. V., An introduction to transform theory, (Academic Press, 1971).Google Scholar
8.Whittaker, E. T. and Watson, G. N., A course of modem analysis, (Cambridge University Press, 1963).Google Scholar