Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Valiquette, Francis
2012.
Geometric affine symplectic curve flows in R4.
Differential Geometry and its Applications,
Vol. 30,
Issue. 6,
p.
631.
Li, YanYan
and
Qu, ChangZheng
2015.
Symplectic invariants for curves and integrable systems in similarity symplectic geometry.
Science China Mathematics,
Vol. 58,
Issue. 7,
p.
1415.
Asadi, Esmaeel
Ranjbar Niari, Zari
and
Noori, Saeideh
2025.
Darboux–Bäcklund transformations, generalized Bianchi’s permutability theorem and exact solutions of a novel coupled modified Korteweg–de Vries system.
Journal of Mathematical Physics,
Vol. 66,
Issue. 1,


 =
= 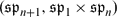 . The integrability structure is shown to be geometrically encoded by a Poisson–Nijenhuis structure and a symplectic operator.
. The integrability structure is shown to be geometrically encoded by a Poisson–Nijenhuis structure and a symplectic operator.