Article contents
Infinite dimensional representations of 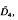
Published online by Cambridge University Press: 18 May 2009
Extract
By a representation of the extended Dynkin diagram 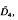 we shall mean a list of 5 vector spaces P, E1, E2, E3, E4 over an algebraically closed field K, and 4 linear maps a1, a2, a3, a4 as shown.
we shall mean a list of 5 vector spaces P, E1, E2, E3, E4 over an algebraically closed field K, and 4 linear maps a1, a2, a3, a4 as shown.
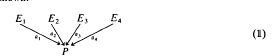
The spaces need not be of finite dimension.
In their solution of the 4-subspace problem [6], Gelfand and Ponomarev have classified such representations when the spaces are finite dimensional. A representation like (1) can also be viewed as a module over the K-algebra R4 consisting of all 5 × 5 matrices having zeros off the first row and off the main diagonal.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1990
References
REFERENCES
- 2
- Cited by


